题目内容
已知sinα-sinβ=
,cosα-cosβ=
,则cos2
等于( )
| ||
| 3 |
| ||
| 3 |
| α-β |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:二倍角的余弦
专题:三角函数的求值
分析:将已知中的两等式分别平方后相加,可求得cos(α-β)=
,利用二倍角的余弦即可求得cos2
的值.
| 1 |
| 2 |
| α-β |
| 2 |
解答:
解:∵(sinα-sinβ)2=
,(cosα-cosβ)2=
,
两式相加得:2-2sinαsinβ-2cosαcosβ=1,
∴cos(α-β)=
,
∴cos2
=
=
.
故选:A.
| 2 |
| 3 |
| 1 |
| 3 |
两式相加得:2-2sinαsinβ-2cosαcosβ=1,
∴cos(α-β)=
| 1 |
| 2 |
∴cos2
| α-β |
| 2 |
| 1+cos(α-β) |
| 2 |
| 3 |
| 4 |
故选:A.
点评:本题考查三角函数间的平方关系式的应用,逆用两角差的余弦,突出考查二倍角的余弦,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知等差数列{an}的前n项和为Sn(n∈N*),且an=2n+λ,若数列{Sn}为递增数列,则实数λ的取值范围为( )
| A、[-3,+∞) |
| B、(-3,+∞) |
| C、(-4,+∞) |
| D、[-4,+∞) |
 在斜三棱柱ABC-A1B1C1中,A0,B0分别为侧棱AA1,BB1上的点,且知BB0=A0A1,过A0,B0,C1的截面将三棱柱分成上下两个部分体积之比为( )
在斜三棱柱ABC-A1B1C1中,A0,B0分别为侧棱AA1,BB1上的点,且知BB0=A0A1,过A0,B0,C1的截面将三棱柱分成上下两个部分体积之比为( )| A、2:1 | B、4:3 |
| C、3:2 | D、1:1 |
已知函数f(x)(x∈R)的图象上任一点(x0,y0)处切线的方程为:y-y0=(x0-2)( x0-1)(x-x0),那么函数f(x)的单调减区间是( )
| A、(1,2) |
| B、(-∞,1] |
| C、[2,+∞) |
| D、(-∞,-1) |
关于二项式(x-1)23有下列命题:
①该二项展开式中非常数项的系数和是1;
②该二项展开式中第六项为
x6;
③该二项展开式中系数最大的项是第13项;
④当x=24时,(x-1)23除以24的余数是23.
其中正确命题有( )
①该二项展开式中非常数项的系数和是1;
②该二项展开式中第六项为
| C | 6 23 |
③该二项展开式中系数最大的项是第13项;
④当x=24时,(x-1)23除以24的余数是23.
其中正确命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
函数f(x)=sinωx(ω>0)的图象在y轴右边的第一条对称轴的方程x=1,则ω=( )
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
在三棱椎P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上的一点,它的正视图和侧视图如图所示,则下列命题正确的是( )
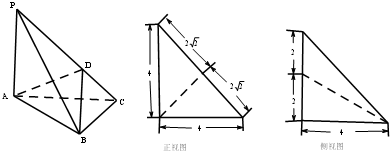

A、AD⊥平面PBC且三棱椎D-ABC的体积为
| ||
B、BD⊥平面PAC且三棱椎D-ABC的体积为
| ||
C、AD⊥平面PBC且三棱椎D-ABC的体积为
| ||
D、BD⊥平面PAC且三棱椎D-ABC的体积为
|
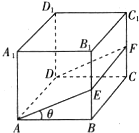 如图正方体ABCD-A1B1C1D1的棱长为1,点E在线段BB1和线段A1B1上移动,∠EAB=θ,θ∈(0,
如图正方体ABCD-A1B1C1D1的棱长为1,点E在线段BB1和线段A1B1上移动,∠EAB=θ,θ∈(0,