题目内容
一个四棱柱的各个顶点都在一个直径为2cm的球面上,如果该四棱柱的底面为边长是1cm的正方形,侧棱与底面垂直,那么该四棱柱的表面积为 cm2.
考点:棱柱、棱锥、棱台的侧面积和表面积
专题:计算题,空间位置关系与距离
分析:四棱柱为正四棱柱,设正四棱柱的侧棱长为l,根据正四棱柱的体对角线长等于外接球的直径,求出棱柱的侧棱长,代入棱柱的表面积公式计算.
解答:
解:由已知得:四棱柱为正四棱柱,设正四棱柱的侧棱长为l,
则正四棱柱的体对角线长等于外接球的直径,即
=2,∴l=
,
∴四棱柱的表面积S=2×1×1+4×1×
=4
+2.
故答案为:4
+2.
则正四棱柱的体对角线长等于外接球的直径,即
| 1+1+l2 |
| 2 |
∴四棱柱的表面积S=2×1×1+4×1×
| 2 |
| 2 |
故答案为:4
| 2 |
点评:不同考查了棱柱的表面积及接体问题,关键是利用外接球的直径求得棱柱的侧棱长.

练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn(n∈N*),且an=2n+λ,若数列{Sn}为递增数列,则实数λ的取值范围为( )
| A、[-3,+∞) |
| B、(-3,+∞) |
| C、(-4,+∞) |
| D、[-4,+∞) |
 在斜三棱柱ABC-A1B1C1中,A0,B0分别为侧棱AA1,BB1上的点,且知BB0=A0A1,过A0,B0,C1的截面将三棱柱分成上下两个部分体积之比为( )
在斜三棱柱ABC-A1B1C1中,A0,B0分别为侧棱AA1,BB1上的点,且知BB0=A0A1,过A0,B0,C1的截面将三棱柱分成上下两个部分体积之比为( )| A、2:1 | B、4:3 |
| C、3:2 | D、1:1 |
函数f(x)=sinωx(ω>0)的图象在y轴右边的第一条对称轴的方程x=1,则ω=( )
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
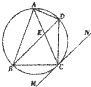 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.若AB=6,BC=4,则DE=
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.若AB=6,BC=4,则DE=