题目内容
若不等式|x+1|-|x-2|≥a在实数集R中有非空真子集解,则a的取值范围是 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:令f(x)=|x+1|-|x-2|,易求f(x)∈[-3,3],由于不等式|x+1|-|x-2|≥a在实数集R中有非空真子集解,对a=-3与a=3讨论,即可求得a的取值范围.
解答:
解:令f(x)=|x+1|-|x-2|,
则f(x)=
,
∴f(x)∈[-3,3],
∵不等式|x+1|-|x-2|≥a在实数集R中有非空真子集解,
当a=-3时,|x+1|-|x-2|≥-3恒成立,即x∈R,与题意不符,故a≠-3,
当a=3时,当x≥2时满足题意,
∴-3<a≤3.
故答案为:-3<a≤3.
则f(x)=
|
∴f(x)∈[-3,3],
∵不等式|x+1|-|x-2|≥a在实数集R中有非空真子集解,
当a=-3时,|x+1|-|x-2|≥-3恒成立,即x∈R,与题意不符,故a≠-3,
当a=3时,当x≥2时满足题意,
∴-3<a≤3.
故答案为:-3<a≤3.
点评:本题考查绝对值不等式的解法,考查分类讨论思想的应用,考查抽象思维与逻辑思维的应用,属于难题.

练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn(n∈N*),且an=2n+λ,若数列{Sn}为递增数列,则实数λ的取值范围为( )
| A、[-3,+∞) |
| B、(-3,+∞) |
| C、(-4,+∞) |
| D、[-4,+∞) |
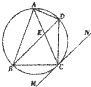 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.若AB=6,BC=4,则DE=
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.若AB=6,BC=4,则DE=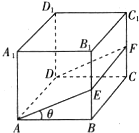 如图正方体ABCD-A1B1C1D1的棱长为1,点E在线段BB1和线段A1B1上移动,∠EAB=θ,θ∈(0,
如图正方体ABCD-A1B1C1D1的棱长为1,点E在线段BB1和线段A1B1上移动,∠EAB=θ,θ∈(0,