题目内容
设函数f(x)=2lnx+
ax2-(2a+1)x(a>0)
(1)当a=1时,求函数f(x)的单调区间;
(2)求f(x)在(0,2]上的最大值.
| 1 |
| 2 |
(1)当a=1时,求函数f(x)的单调区间;
(2)求f(x)在(0,2]上的最大值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)通过求函数导数,然后判断f′(x)的符号即可.
(Ⅱ)求出原函数的导函数,结合二次函数的图象和性质,分①
≥2与②0<
<2两种情况,分析函数y=f(x)在区间(0,2]上的单调性,可得答案.
(Ⅱ)求出原函数的导函数,结合二次函数的图象和性质,分①
| 1 |
| a |
| 1 |
| a |
解答:
解:(1)f(x)的定义域为(0,+∞),f′(x)=
+ax-(2a+1)=
,
当a=1时,f′(x)=
,由f′(x)>0得x>2或0<x<1,由f′(x)<0得1<x<2,
所以增区间为(0,1)与(2,+∞),减区间为(1,2).
(2)由f′(x)=0得x=2或x=
,
①当
≥2时,即0<a≤
时,f(x)在(0,2]上单调递增,f(x)max=f(2)=2ln2-2a-2,
②当0<
<2时,即a>
时,f(x)在(0,
]上单调递增,在(
,2]上单调递减,f(x)max=f(
)=2ln
-
-2,
综上所述得f(x)max=
.
| 2 |
| x |
| ax2-(2a+1)x+2 |
| x |
当a=1时,f′(x)=
| x2-3x+2 |
| x |
所以增区间为(0,1)与(2,+∞),减区间为(1,2).
(2)由f′(x)=0得x=2或x=
| 1 |
| a |
①当
| 1 |
| a |
| 1 |
| 2 |
②当0<
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| 2a |
综上所述得f(x)max=
|
点评:本题考查的知识点是导数法判断函数的单调性,熟练掌握导数的符号与原函数单调性的关系是解答的关键.

练习册系列答案
相关题目
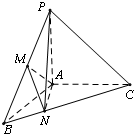 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=| 1 |
| 3 |
(1)求证:MN⊥AB;
(2)求平面MAN与平面PAN的夹角的余弦值.
设f(x)=cos(
+
),则f(1)+f(2)+f(3)+…+f(2010)=( )
| nπ |
| 2 |
| π |
| 4 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|