题目内容
函数y=
的最大值是 ．
| 5-2sinx |
| 2+sinx |
考点：三角函数的最值
专题：计算题,三角函数的图像与性质
分析：将函数化为：y=-2+
，再由正弦函数的值域，即可得到最大值．
| 9 |
| 2+sinx |
解答：
解：y=
=-2+
，
当sinx=-1，即x=2kπ-
，k∈Z，
y取得最大值，且为-2+9=7．
故答案为：7．
| 5-2sinx |
| 2+sinx |
=-2+
| 9 |
| 2+sinx |
当sinx=-1，即x=2kπ-
| π |
| 2 |
y取得最大值，且为-2+9=7．
故答案为：7．
点评：本题考查分式函数的最值，考查正弦函数的值域的运用，考查运算能力，属于中档题．
练习册系列答案
优学名师名题系列答案
相关题目
如图所示，平面四边形ABCD中，AB=AD=CD=1，BD=| 2 |
BD⊥CD，将其沿对角线BD折成四面体A-BCD，使平面ABD⊥平面BCD，则下列说法中不正确的是（ ）
| A、平面ACD⊥平面ABD |
| B、AB⊥CD |
| C、平面ABC⊥平面ACD |
| D、AB∥平面ABC |
等比数列{an}的首项a1=1002，公比q=
，记Pn=a1•a2•…•an，则Pn达到最大值时，n的值为（ ）
| 1 |
| 2 |
| A、8 | B、9 | C、10 | D、11 |
已知圆的方程为x2+y2-6x-8y=0．设该圆过点（-1，4）的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积为（ ）
| A、15 | B、30 | C、45 | D、60 |
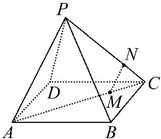如图，四棱锥P-ABCD中，M，N分别为AC，PC上的点，且MN∥平面PAD，则（ ）| A、MN∥PD |
| B、MN∥PA |
| C、MN∥AD |
| D、以上均有可能 |
函数f（x）=sinx+cos2x的图象为（ ）
A、 |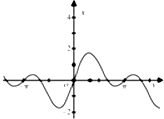
B、 |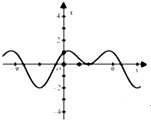
C、 |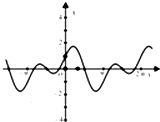
D、 |