题目内容
已知圆锥的表面积为a m2,且它的侧面展开图是一个半圆,求这个圆锥的底面直径和体积.
考点:棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:首先,设圆锥母线长R,底面园半径长r,然后,根据侧面展开图得到R=2r,然后,求解其底面直径和体积.
解答:
解:设圆锥母线长R,底面园半径长r,
∵侧面展开图是一个半圆,此半圆半径为R,半圆弧长为2πr,
∴πR=2πr,
∴R=2r,
∵表面积是侧面积与底面积的和,
∴S表=
πR2+πr2
∵R=2r
∴S表=3πr2=a,
∴r=
,
∴圆锥的底面直径2r=2
,
∵圆锥的高为:h=
=
r,
∴V=
πr2h=
πr2
r
=
πr3=
,
∴圆锥的体积为
.
∵侧面展开图是一个半圆,此半圆半径为R,半圆弧长为2πr,
∴πR=2πr,
∴R=2r,
∵表面积是侧面积与底面积的和,
∴S表=
| 1 |
| 2 |
∵R=2r
∴S表=3πr2=a,
∴r=
|
∴圆锥的底面直径2r=2
|
∵圆锥的高为:h=
| R2-r2 |
| 3 |
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
=
| ||
| 3 |
a
| ||
| 9 |
∴圆锥的体积为
a
| ||
| 9 |
点评:本题重点考查了圆锥的结构特征、圆锥的表面积公式和体积公式及其灵活运用,属于中档题,解题关键是找到母线长和底面圆半径之间的关系.

练习册系列答案
相关题目
等比数列{an}的首项a1=1002,公比q=
,记Pn=a1•a2•…•an,则Pn达到最大值时,n的值为( )
| 1 |
| 2 |
| A、8 | B、9 | C、10 | D、11 |
函数f(x)=sinx+cos2x的图象为( )
A、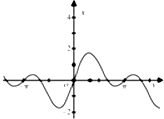 |
B、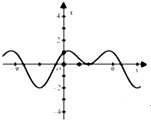 |
C、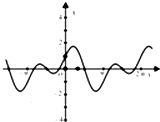 |
D、 |
曲线
+
=1(a<6)与曲线
+
=1(5<b<9)有( )
| x2 |
| 10-a |
| y2 |
| 6-a |
| x2 |
| 5-b |
| y2 |
| 9-b |
| A、相同的离心率 |
| B、相同的准线 |
| C、相同的焦点 |
| D、相同的焦距 |