题目内容
已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2+2x，若f（2-a2）＞f（a），则实数a的取值范围是（ ）
| A、（-∞，-1 ）∪（2，+∞） |
| B、（-1，2） |
| C、（-2，1 ） |
| D、（-∞，-2 ）∪（1，+∞） |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：由题意可先判断出f（x）=x2+2x=（x+1）2-1在（0，+∞）上单调递增，根据奇函数的对称区间上的单调性可知，f（x）在（-∞，0）上单调递增，从而可比较2-a2与a的大小，解不等式可求a的范围
解答：
解：∵f（x）=x2+2x=（x+1）2-1在（0，+∞）上单调递增
又∵f（x）是定义在R上的奇函数
根据奇函数的对称区间上的单调性可知，f（x）在（-∞，0）上单调递增
∴f（x）在R上单调递增
∵f（2-a2）＞f（a）
∴2-a2＞a
解不等式可得，-2＜a＜1
故选C
又∵f（x）是定义在R上的奇函数
根据奇函数的对称区间上的单调性可知，f（x）在（-∞，0）上单调递增
∴f（x）在R上单调递增
∵f（2-a2）＞f（a）
∴2-a2＞a
解不等式可得，-2＜a＜1
故选C
点评：本题主要考查了奇函数在对称区间上的单调性相同（偶函数对称区间上的单调性相反）的性质的应用，一元二次不等式的求解，属于基础试题
练习册系列答案
出彩同步大试卷系列答案
相关题目
在△ABC中，若AB=4，BC=2
，且
•
=-8，则AC等于（ ）
| 2 |
| BA |
| BC |
A、4
| ||
| B、4 | ||
C、2
| ||
D、2
|
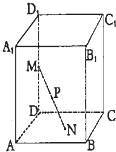已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3，∠BAD=60°长为2的线段MN的一个端点M在DD1上运动，另一个端点N在底面ABCD上运动，则MN的中点P的轨迹（曲面）与共一顶点D的三个面所围成的几何体的体积为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
有穷数列1，23，26，29，…，23n+6的项数是（ ）
| A、3n+7 | B、3n+6 |
| C、n+3 | D、n+2 |