题目内容
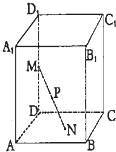 已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3,∠BAD=60°长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为( )
已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3,∠BAD=60°长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由题意知P点的轨迹是以D为球心半径为1的球被平行六面体截得的曲面,它的体积是该球体积的
×
=
,由此能求出MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
解答:
解:∵△MDN为直角三角形,P为MN的中点,
∴DP=
MN=1.
∴P点的轨迹是以D为球心半径为1的球被平行六面体截得的曲面,
由题意得∠ADC=120°=
,
∴它的体积是该球体积的
×
=
,
∴MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为:
V=
×
×13=
.
故选:A.
∴DP=
| 1 |
| 2 |
∴P点的轨迹是以D为球心半径为1的球被平行六面体截得的曲面,
由题意得∠ADC=120°=
| 2π |
| 3 |
∴它的体积是该球体积的
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为:
V=
| 1 |
| 6 |
| 4π |
| 3 |
| 2π |
| 9 |
故选:A.
点评:本题考查几何体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
不等式|4-x2|+
≥0的解集是( )
| |x| |
| x |
A、{x|x≤-
| ||||
| B、{x|x>0} | ||||
C、{x|x≤-
| ||||
D、{x|x≤-
|
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2+2x,若f(2-a2)>f(a),则实数a的取值范围是( )
| A、(-∞,-1 )∪(2,+∞) |
| B、(-1,2) |
| C、(-2,1 ) |
| D、(-∞,-2 )∪(1,+∞) |
已知圆锥的母线长l=5cm,高h=4cm,则该圆锥的体积是( )cm3.
| A、12π | B、8π |
| C、13π | D、16π |
函数y=2sin(
-x)的一个单调增区间是( )
| π |
| 4 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
已知函数f(x)=
,若对于任意x∈R,不等式f(x)≤
-t+1恒成立,则实数t的取值范围是( )
|
| t2 |
| 4 |
| A、(-∞,1]∪[2,+∞) |
| B、(-∞,1]∪[3,+∞) |
| C、[1,3] |
| D、(-∞,2]∪[3,+∞) |