题目内容

在△ABC中，若AB=4，BC=2
2
，且
BA
•
BC
=-8，则AC等于（　　）
A、4
2
B、4
C、2
2
D、2
10
考点：余弦定理,平面向量数量积的运算
专题：解三角形,平面向量及应用
分析：利用余弦定理和向量的数量积代入计算即可．
解答： 解：∵
BA
•
BC
=-8，
∴
BA
•
BC
=cosB|BA||BC|=-8，
根据余弦定理，
∴AC2=BA2+BC2-2cosB|BA||BC|=16+8+8=32，
∴AC=4
2
，
故选：A．
点评：本题考查了数量积运算、余弦定理的应用，属于基础题．
练习册系列答案
相关题目
已知数列{an}的前n项和为Sn，且an是Sn与1的等差中项，数列{bn}中，b1=2，点P（bn，bn+1）在直线y=x+2上．
（1）求证：数列{an}是等比数列，并求通项公式；
（2）求数列{bn}的通项bn；
（3）设cn=an•bn，求数列{cn}的前n项和Tn．
用数学归纳法证明，若f（n）=1+
1
2
+
1
3
+…+
1
n
，则n+f（1）+f（2）+…+f（n-1）=n•f（n）（n≥2，且n∈N+）．
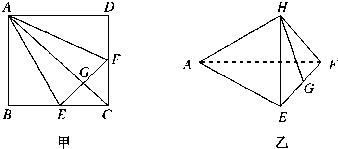
如图甲所示，在正方形ABCD中，EF分别是BC、CD的中点，G是EF的中点，现在沿AE、AF及EF把这个正方形折成一个四面体，使B、C、D三点重合，重合后的点记为H，如图乙所示，那么，在四面体A-EFH中必有（　　）
A、AH⊥△EFH所在平面
B、AG⊥△EFH所在平面
C、HF⊥△AEF所在平面
D、HG⊥△AEF所在平面
编写一个程序，输入梯形的上底、下底和高的值，计算并输出其面积．
对任意实数x，＜x＞表示不小于x的最小整数，如＜1.1＞=2，＜-1.1＞=-1，则“|x-y|＜1”是“＜x＞=＜y＞”的（　　）条件．
A、充分不必要
B、必要不充分
C、充分
D、既不充分又不必要
不等式|4-x2|+
|x|
x
≥0的解集是（　　）
A、{x|x≤-
5
或x≥
5
}
B、{x|x＞0}
C、{x|x≤-
5
或-
3
≤x＜0}
D、{x|x≤-
5
或-
3
≤x＜0或x＞0}
如图，在直三棱柱ABC-A1B1C1中，D、E分别是BC和CC1的中点，已知AB=AC=AA1=4，∠BAC=90°．
（1）求证：B1D⊥平面AED；
（2）求二面角B1-AE-D的余弦值；
（3）求三棱锥A-B1DE的体积．
已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2+2x，若f（2-a2）＞f（a），则实数a的取值范围是（　　）
A、（-∞，-1 ）∪（2，+∞）
B、（-1，2）
C、（-2，1 ）
D、（-∞，-2 ）∪（1，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网