题目内容
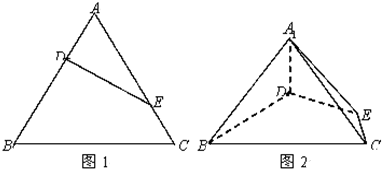
等边三角形ABC的边长为3,点D、E分别是边AB、AC上的点,且满足
=
=
(如图1).将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B为直二面角,连结A1B、A1C (如图2).
(Ⅰ)求证:A1D⊥平面BCED;
(Ⅱ)若P是线段BC上的点,且三棱锥D-A1EP的体积为
,求BP长.
| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |
(Ⅰ)求证:A1D⊥平面BCED;
(Ⅱ)若P是线段BC上的点,且三棱锥D-A1EP的体积为
| ||
| 6 |

考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)由已知得AD=1,AE=2,又∠DAE=60°,二面角A1-DE-B为直二面角,由此能证明A1D⊥平面BDEC.
(Ⅱ)由设PB=x,由(1)知VD-A1EP=VA1-DEP=
•A1D•S△DEP=
,由此能求出BP.
(Ⅱ)由设PB=x,由(1)知VD-A1EP=VA1-DEP=
| 1 |
| 3 |
| ||
| 6 |
解答:
(Ⅰ)证明:等边三角形ABC的边长为3,
且
=
=
,
∴AD=1,AE=2,又∠DAE=60°,
∴DE=
⇒DE⊥AB⇒DE⊥A1D,
又二面角A1-DE-B为直二面角,
平面A1DE∩平面BDE=DE,
∴A1D⊥DE,A1D⊥BD,∴A1D⊥平面BDEC.
(Ⅱ)解:设PB=x,
由(1)知VD-A1EP=VA1-DEP=
•A1D•S△DEP=
,
∴S△DEP=
,
又在△ABC中,
S△DEP=S△ABC-S△DBP-S△ECP-S△ADE
=
-
x-
(3-x)-
,解得:x=2,
∴BP=2.
且
| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |
∴AD=1,AE=2,又∠DAE=60°,
∴DE=
| 3 |
又二面角A1-DE-B为直二面角,
平面A1DE∩平面BDE=DE,
∴A1D⊥DE,A1D⊥BD,∴A1D⊥平面BDEC.
(Ⅱ)解:设PB=x,
由(1)知VD-A1EP=VA1-DEP=
| 1 |
| 3 |
| ||
| 6 |
∴S△DEP=
| ||
| 2 |
又在△ABC中,
S△DEP=S△ABC-S△DBP-S△ECP-S△ADE
| ||
| 2 |
9
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
∴BP=2.
点评:本题考查直线与平面垂直的证明,考查线段长的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
如图甲所示,在正方形ABCD中,EF分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为H,如图乙所示,那么,在四面体A-EFH中必有( )
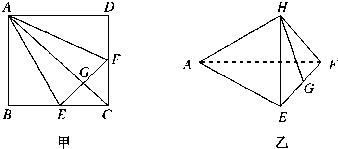

| A、AH⊥△EFH所在平面 |
| B、AG⊥△EFH所在平面 |
| C、HF⊥△AEF所在平面 |
| D、HG⊥△AEF所在平面 |
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2+2x,若f(2-a2)>f(a),则实数a的取值范围是( )
| A、(-∞,-1 )∪(2,+∞) |
| B、(-1,2) |
| C、(-2,1 ) |
| D、(-∞,-2 )∪(1,+∞) |
函数y=2sin(
-x)的一个单调增区间是( )
| π |
| 4 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
 如图,在直三棱柱ABC-A1B1C1中,D、E分别是BC和CC1的中点,已知AB=AC=AA1=4,∠BAC=90°.
如图,在直三棱柱ABC-A1B1C1中,D、E分别是BC和CC1的中点,已知AB=AC=AA1=4,∠BAC=90°.