题目内容
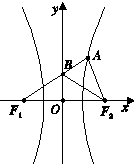 如图,双曲线C:
如图,双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、1+
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:运用等腰三角形的性质,以及三角形的内角和定理,可得|BF1|=|BF2|,∠BF2F1=36°,再由双曲线的定义可得|AF2|=2c-2a,再由内角平分线定理可得
=
,化简整理,结合离心率公式解方程,即可得到.
| 2a |
| 2c-2a |
| 2c-2a |
| 2c |
解答:
解: 由F2B是∠AF2F1的角平分线,O为F1F2的中点,
由F2B是∠AF2F1的角平分线,O为F1F2的中点,
则|BF1|=|BF2|,
∠BF1F2=∠BF2F1=∠BF2A,设为α.
又|AF1|=2c,则∠A=2α,
则∠A+∠AF1F2+∠AF2F1=5α=180°,
即有α=36°,
∠ABF2=2α=72°=∠A,
即有|BF2|=|AF2|,
由双曲线的定义可得|AF1|-|AF2|=2a,
则|AF2|=2c-2a,|AB|=2c-(2c-2a)=2a,
由F2B是∠AF2F1的角平分线,可得
=
,
即有
=
,
即有ac=(c-a)2,
即c2-3ac+a2=0,
由e=
,可得e2-3e+1=0,
解得e=
或
,
由于e>1,则e=
.
故选:D.
 由F2B是∠AF2F1的角平分线,O为F1F2的中点,
由F2B是∠AF2F1的角平分线,O为F1F2的中点,则|BF1|=|BF2|,
∠BF1F2=∠BF2F1=∠BF2A,设为α.
又|AF1|=2c,则∠A=2α,
则∠A+∠AF1F2+∠AF2F1=5α=180°,
即有α=36°,
∠ABF2=2α=72°=∠A,
即有|BF2|=|AF2|,
由双曲线的定义可得|AF1|-|AF2|=2a,
则|AF2|=2c-2a,|AB|=2c-(2c-2a)=2a,
由F2B是∠AF2F1的角平分线,可得
| |AB| |
| |BF1| |
| |AF2| |
| |F1F2| |
即有
| 2a |
| 2c-2a |
| 2c-2a |
| 2c |
即有ac=(c-a)2,
即c2-3ac+a2=0,
由e=
| c |
| a |
解得e=
3+
| ||
| 2 |
3-
| ||
| 2 |
由于e>1,则e=
3+
| ||
| 2 |
故选:D.
点评:本题考查双曲线的定义、方程和性质,主要考查离心率的求法,运用等腰三角形的性质和内角平分线定理是解题的关键.

练习册系列答案
相关题目
已知向量
=(2,3),
=(-2,x),若
在
方向上的投影等于-
,则实数x的值为( )
| a |
| b |
| a |
| b |
| ||
| 5 |
A、
| ||
| B、1 | ||
C、1或
| ||
| D、2 |
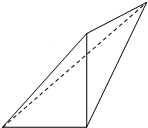 一个四面体如图,若该四面体的正视图(主视图)、侧视图(左视图)和俯视图都是直角边长为1的等腰直角三角形,则它的体积V=( )
一个四面体如图,若该四面体的正视图(主视图)、侧视图(左视图)和俯视图都是直角边长为1的等腰直角三角形,则它的体积V=( )A、
| ||
B、
| ||
C、
| ||
D、
|
若双曲线
-
=1(a>0,b>0)与直线y=
x无交点,则
的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| b |
| a |
A、(0,
| ||
B、(0,
| ||
C、(
| ||
D、[
|
记集合A={(x,y)|
}、B={(x,y)|x2+y2≤1}构成的平面区域分别为M、N,现随机地向N中抛一粒豆子(大小忽略不计),则该豆子落入M中的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
在平行四边形ABCD中,AC为一条对角线,
=(2,4),
=(1,3),则
等于( )
| AB |
| AC |
| BD |
| A、(2,4) |
| B、(3,5) |
| C、(-3,-5) |
| D、(-2,-4) |