Question

7．已知函数f（x）=$\left\{\begin{array}{l}{\frac{1}{2}-|x-\frac{3}{2}|（x≤2）}\\{{e}^{x-2}（-{x}^{2}+8x-12）（x＞2）}\end{array}\right.$，若在区间（1，∞）上存在n（n≥2）个不同的数x₁，x₂，x₃，…，x_n，使得$\frac{f（{x}_{1}）}{{x}_{1}}$=$\frac{f（{x}_{2}）}{{x}_{2}}$=…$\frac{f（{x}_{n}）}{{x}_{n}}$成立，则n的取值集合是（　　）

• A． {2，3，4，5}
• B． {2，3}
• C． {2，3，5}
• D． {2，3，4}

Answer 1

分析 由题意可知n为方程f（x）=kx的解的个数，判断f（x）的单调性，作出y=f（x）与y=kx的函数图象，根据图象交点个数判断．

解答 解：设$\frac{f（{x}_{1}）}{{x}_{1}}$=$\frac{f（{x}_{2}）}{{x}_{2}}$=…$\frac{f（{x}_{n}）}{{x}_{n}}$=k，则方程$\frac{f（x）}{x}=k$有n个根，
即f（x）=kx有n个根，
f（x）=$\left\{\begin{array}{l}{x-1，x≤\frac{3}{2}}\\{-x+2，\frac{3}{2}＜x≤2}\\{{e}^{x-2}（-{x}^{2}+8x-12），x＞2}\end{array}\right.$，
∴f（x）在（1，$\frac{3}{2}$）上单调递增，在（$\frac{3}{2}$，2）上单调递减．
当x＞2时，f′（x）=e^x-2（-x²+8x-12）+e^x-2（-2x+8）=e^x-2（-x²+6x-4），
设g（x）=-x²+6x-4（x＞2），令g（x）=0得x=3+$\sqrt{5}$，
∴当2$＜x＜3+\sqrt{5}$时，g（x）＞0，当x＞3+$\sqrt{5}$时，g（x）＜0，
∴f（x）在（2，3+$\sqrt{5}$）上单调递增，在（3+$\sqrt{5}$，+∞）上单调递减，
作出f（x）与y=kx的大致函数图象如图所示：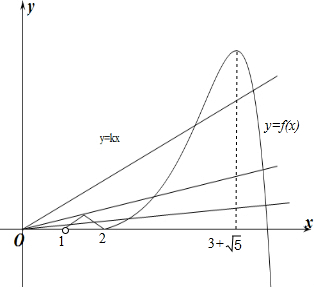

由图象可知f（x）=kx的交点个数可能为1，2，3，4，
∵n≥2，故n的值为2，3，4．
故选D．

点评 本题考查了方程的解与函数图象的关系，函数的单调性判断，属于中档题．