题目内容
已知数列{an}中,a1=
,an=2-
(n≥2,n∈N*),数列{bn}满足bn=
(n∈N*).
(1)求证:数列{bn}是等差数列;
(2)求{bn}的通项公式及前n项和.
| 3 |
| 5 |
| 1 |
| an-1 |
| 1 |
| an-1 |
(1)求证:数列{bn}是等差数列;
(2)求{bn}的通项公式及前n项和.
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:本题(1)利用等差数列的定义,证明数列{bn}是等差数列;(2)利用等差数列的通项公式和前n项和公式,求数列{bn}的通项公式及前n项和.
解答:
解:(1)∵an=2-
(n≥2,n∈N*),
∴an=2-
=
,
∵数列{bn}满足bn=
(n∈N*),
∴当n≥2,n∈N*时,
bn-bn-1=
-
=
-
=
-
=
=1(常数).
∴数列{bn}是等差数列.
(2)∵a1=
,bn=
(n∈N*),
∴b1=
=-
.
由(1)知:数列{bn}是等差数列,
∴bn=-
+(n-1)×1=n-
,(n∈N*),
Sn=-
n+
×1=
n2-3n,(n∈N*).
| 1 |
| an-1 |
∴an=2-
| 1 |
| an-1 |
| 2an-1-1 |
| an-1 |
∵数列{bn}满足bn=
| 1 |
| an-1 |
∴当n≥2,n∈N*时,
bn-bn-1=
| 1 |
| an-1 |
| 1 |
| an-1-1 |
=
| 1 | ||
|
| 1 |
| an-1-1 |
=
| an-1 |
| an-1-1 |
| 1 |
| an-1-1 |
=
| an-1-1 |
| an-1-1 |
=1(常数).
∴数列{bn}是等差数列.
(2)∵a1=
| 3 |
| 5 |
| 1 |
| an-1 |
∴b1=
| 1 | ||
|
| 5 |
| 2 |
由(1)知:数列{bn}是等差数列,
∴bn=-
| 5 |
| 2 |
| 7 |
| 2 |
Sn=-
| 5 |
| 2 |
| n(n-1) |
| 2 |
| 1 |
| 2 |
点评:本题考查了等差数列的定义、通项公式和前n项和公式,本题难度不大,属于基础题.

练习册系列答案
相关题目
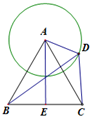 △ABC是边长为2的等边三角形,D是以A为圆心,半径为1的圆上任意一点,如图所示,则
△ABC是边长为2的等边三角形,D是以A为圆心,半径为1的圆上任意一点,如图所示,则| BD |
| CD |
A、3+
| ||
B、3-
| ||
C、3-2
| ||
D、3+2
|
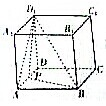 如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.
如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.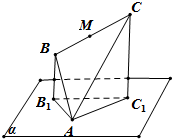 如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,M为BC的中点.若△ABC在平面α上的射影是以A为直角顶点的三角形AB1C1,则M到平面α的距离的取值范围是
如图,边长为4的正△ABC顶点A在平面α上,B,C在平面α的同侧,M为BC的中点.若△ABC在平面α上的射影是以A为直角顶点的三角形AB1C1,则M到平面α的距离的取值范围是