Question

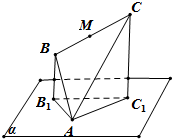如图，边长为4的正△ABC顶点A在平面α上，B，C在平面α的同侧，M为BC的中点．若△ABC在平面α上的射影是以A为直角顶点的三角形AB₁C₁，则M到平面α的距离的取值范围是

 

．

Answer 1

考点：点、线、面间的距离计算

专题：计算题,空间位置关系与距离

分析：设出B，C到面的距离，则M到平面α的距离为两者和的一半，确定ab=8，即可求出M到平面α的距离的取值范围．

解答： 解：设B，C到平面α距离分别为a，b，则M到平面α距离为h=

a+b

2

射影三角形两直角边的平方分别16-a²，16-b²，
设线段BC射影长为c，则16-a²+16-b²=c²，（1）
又线段AM射影长为

c

2

，所以（

c

2

）²+

(a+b)2

4

=12，（2）
由（1）（2）联立解得ab=8，
∵a＜4，b＜4，
∴2＜a＜4，
∴h=

1

2

（a+

8

a

）∈[2

2

，3)，
故答案为：[2

2

，3)．

点评：本题考查M到平面α的距离的取值范围，考查学生分析解决问题的能力，确定ab=8是关键．