题目内容
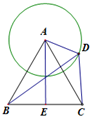△ABC是边长为2的等边三角形，D是以A为圆心，半径为1的圆上任意一点，如图所示，则| BD |
| CD |
A、3+
| ||
B、3-
| ||
C、3-2
| ||
D、3+2
|
考点：向量在几何中的应用
专题：计算题,平面向量及应用
分析：由题意，建立平面直角坐标系，设出点的坐标，从而求最大值．
解答：
解：如图建立平面直角坐标系，
A（0，0），D（cosa，sina），B（-1，-
），C（1，-
）；
则
•
=（cosa+1，sina+
）•（cosa-1，sina+
）
=cos2a-1+（sina+
）2
=2
sina+3，
故当sina=1时有最大值，
即
•
的最大值是2
+3．
故选D．
解：如图建立平面直角坐标系，A（0，0），D（cosa，sina），B（-1，-
| 3 |
| 3 |
则
| BD |
| CD |
| 3 |
| 3 |
=cos2a-1+（sina+
| 3 |
=2
| 3 |
故当sina=1时有最大值，
即
| BD |
| CD |
| 3 |
故选D．
点评：本题考查了平面向量的应用及学生的作图能力，属于中档题．
练习册系列答案
相关题目
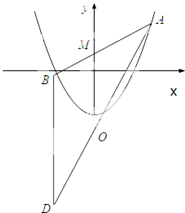如图，已知抛线C：x2=4y，过点M（0，2）任作一直线与C相交于A，B两点，过点B作y轴的平行线与直线AO相交于点D（O为坐标原点）．
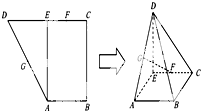如图，已知直角梯形ABCD中，E为CD边中点，且AE⊥CD，又G，F分别为DA，EC的中点，将△ADE沿AE折叠，使得DE⊥EC．已知三棱锥的三视图如图所示，则它的外接球的表面积为（ ）
| A、4π | B、8π |
| C、12π | D、16π |