题目内容
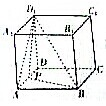 如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.
如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.考点:二面角的平面角及求法
专题:计算题,空间位置关系与距离,空间角
分析:设正方体的边长为2,取BD1的中点E,连接PE,则PE⊥BD1,过E在三角形ABD1中,作EF⊥BD1,交AD1于F,连接FP,
则∠FEP即为二面角A-BD1-P的平面角.由平面几何的知识,分别求出EF,EP,PF 的长,再由余弦定理,即可得到二面角的平面角的大小.
则∠FEP即为二面角A-BD1-P的平面角.由平面几何的知识,分别求出EF,EP,PF 的长,再由余弦定理,即可得到二面角的平面角的大小.
解答:
 解:设正方体的边长为2,
解:设正方体的边长为2,
由于P为AD的中点,
则BP=PD1=
=
,
取BD1的中点E,连接PE,则PE⊥BD1,
由于AB⊥平面ADD1A1,
则AB⊥AD1,
过E在三角形ABD1中,作EF⊥BD1,
交AD1于F,连接FP,
则∠FEP即为二面角A-BD1-P的平面角.
在三角形BD1P中,PE=
=
,
EF=D1Etan∠BD1A=
•
=
,
D1F=
=
,AF=2
-
=
,
FP=
=
.
在三角形FEP中,
cos∠FEP=
=
.
则∠FEP=60°.
即有二面角A-BD1-P的大小为60°.
 解:设正方体的边长为2,
解:设正方体的边长为2,由于P为AD的中点,
则BP=PD1=
| 22+12 |
| 5 |
取BD1的中点E,连接PE,则PE⊥BD1,
由于AB⊥平面ADD1A1,
则AB⊥AD1,
过E在三角形ABD1中,作EF⊥BD1,
交AD1于F,连接FP,
则∠FEP即为二面角A-BD1-P的平面角.
在三角形BD1P中,PE=
(
|
| 2 |
EF=D1Etan∠BD1A=
| 3 |
| 2 | ||
2
|
| ||
| 2 |
D1F=
(
|
3
| ||
| 2 |
| 2 |
3
| ||
| 2 |
| ||
| 2 |
FP=
|
| ||
| 2 |
在三角形FEP中,
cos∠FEP=
(
| ||||||||||
2×
|
=
| ||
| 2 |
则∠FEP=60°.
即有二面角A-BD1-P的大小为60°.
点评:本题主要考查空间二面角的求法,考查空间直线与平面的位置关系,考查运算能力,属于中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
设Sn为数列{an}的前n项和,an=1+2+22+…+2n-1,则Sn的值为( )
| A、2n-1 |
| B、2n-1-1 |
| C、2n-n-2 |
| D、2n+1-n-2 |
 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.