题目内容
已知椭圆C:x2+2y2=4.
(1)求椭圆C的离心率;
(2)已知O为原点,点A(t,2)(t∈R),点B在椭圆C上,若OA⊥OB,求线段AB长度的最小值.
(1)求椭圆C的离心率;
(2)已知O为原点,点A(t,2)(t∈R),点B在椭圆C上,若OA⊥OB,求线段AB长度的最小值.
考点:直线与圆锥曲线的关系,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)利用椭圆的方程化为标准方程,求出几何量a、b、c即可求椭圆C的离心率;
(2)设点A,B的坐标分别为(t,2),(x0,y0),其中x0≠0,通过OA⊥OB,推出t=-
,然后求出|AB|的表达式利用基本不等式即可求解线段AB长度的最小值.
(2)设点A,B的坐标分别为(t,2),(x0,y0),其中x0≠0,通过OA⊥OB,推出t=-
| 2y0 |
| x0 |
解答:
(本小题满分16分)
解:(1)由题意,椭圆C的标准方程为
+
=1.(2分)
所以a2=4,b2=2,从而c2=a2-b2=2.(3分)
因此a=2,c=
.(4分)
故椭圆C的离心率e=
=
.(6分)
(2)设点A,B的坐标分别为(t,2),(x0,y0),其中x0≠0.(8分)
因为OA⊥OB,
所以tx0+2y0=0
解得t=-
.(10分)
又x02+2y02=4,∴y02=
(12分)
所以|AB|2=(x0-t)2+(y0-2)2=(x0+
)2+(y0-2)2
=x02+y02+
+4=x02+
+
+4
=
+
+4(0<x02≤4).(14分)
因为0<x02≤4,所以
+
≥4,当且仅当x02=4时等号成立,所以|AB|2≥8.
故线段AB长度的最小值为2
.(16分)
解:(1)由题意,椭圆C的标准方程为
| x2 |
| 4 |
| y2 |
| 2 |
所以a2=4,b2=2,从而c2=a2-b2=2.(3分)
因此a=2,c=
| 2 |
故椭圆C的离心率e=
| c |
| a |
| ||
| 2 |
(2)设点A,B的坐标分别为(t,2),(x0,y0),其中x0≠0.(8分)
因为OA⊥OB,
所以tx0+2y0=0
解得t=-
| 2y0 |
| x0 |
又x02+2y02=4,∴y02=
| 4-x02 |
| 2 |
所以|AB|2=(x0-t)2+(y0-2)2=(x0+
| 2y0 |
| x0 |
=x02+y02+
| 4y02 |
| x02 |
| 4-x02 |
| 2 |
| 2(4-x02) |
| x02 |
=
| x02 |
| 2 |
| 8 |
| x02 |
因为0<x02≤4,所以
| x02 |
| 2 |
| 8 |
| x02 |
故线段AB长度的最小值为2
| 2 |
点评:本题考查椭圆方程的应用,直线与椭圆的位置关系的应用,考查分析问题解决问题的能力,是中档题.

练习册系列答案
相关题目

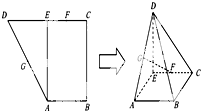 如图,已知直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.
如图,已知直角梯形ABCD中,E为CD边中点,且AE⊥CD,又G,F分别为DA,EC的中点,将△ADE沿AE折叠,使得DE⊥EC.