题目内容
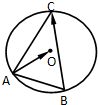
如图，在圆O中，若弦AB=3，弦AC=5，则
•
的值（ ）
| AO |
| BC |
| A、-8 | B、-1 | C、1 | D、8 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：如图所示，过点O作OD⊥BC交BC于点D，连接AD．则D为BC的中点，
•
=0.
=
(
+
)．又
=
+
，
=
-
．即可得出
•
=(
+
)•
=
•
．
| OD |
| BC |
| AD |
| 1 |
| 2 |
| AC |
| AB |
| AO |
| AD |
| DO |
| BC |
| AC |
| AB |
| AO |
| BC |
| AD |
| DO |
| BC |
| AD |
| BC |
解答：
解：如图所示，过点O作OD⊥BC交BC于点D，连接AD．
则D为BC的中点，
•
=0．
∴
=
(
+
)．
又
=
+
，
=
-
．
∴
•
=(
+
)•
=
•
=
(
+
)•(
-
)
=
(
2-
2)
=
(52-32)
=8．
故选：D．
则D为BC的中点，
| OD |
| BC |
∴
| AD |
| 1 |
| 2 |
| AC |
| AB |
又
| AO |
| AD |
| DO |
| BC |
| AC |
| AB |
∴
| AO |
| BC |
| AD |
| DO |
| BC |
=
| AD |
| BC |
=
| 1 |
| 2 |
| AC |
| AB |
| AC |
| AB |
=
| 1 |
| 2 |
| AC |
| AB |
=
| 1 |
| 2 |
=8．
故选：D．
点评：本题考查了垂径定理、向量是三角形法则、平行四边形法则、数量积运算，考查了推理能力与计算能力，属于难题．
练习册系列答案
相关题目
设i是虚数单位，复数
是纯虚数，则实数a=（ ）
| a+i |
| 2-i |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
交通管理部门为了解机动车驾驶员（简称驾驶员）对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查．假设四个社区驾驶员的总人数为N，其中甲社区有驾驶员96人．若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12，22，26，44，则这四个社区驾驶员的总人数N为（ ）
| A、104 | B、808 |
| C、832 | D、2014 |
已知f1（x）=sinx+cosx，fn+1（x）是fn （x）的导函数，即f2（x）=f′1（x），f3（x）=f′2（x），…，fn+1（x）=f′n（x），n∈N*，则f2012（x）=（ ）
| A、sinx+cosx |
| B、sinx-cosx |
| C、-sinx+cosx |
| D、-sinx-cosx |
观察：52-1=24，72-1=48，112-1=120，132-1=168，…所得的结果都是24的倍数，由此推测可有（ ）
| A、其中包含等式：152-1=224 |
| B、一般式是：（2n+3）2-1=4（n+1）（n+2） |
| C、其中包含等式1012-1=10200 |
| D、24的倍数加1必是某一质数的完全平方 |
设集合A=[x||x-1|＜2}，B={y|y2=2x，x∈[0，2]}，则A∩B=（ ）
| A、[0，2] |
| B、（1，3） |
| C、（-1，2] |
| D、（1，4） |
已知{an}是公差不为0的等差数列，且an≥0；又定义bn=
+
（1≤n≤2003 ），则{bn}的最大项是（ ）
| an |
| a2004-n |
| A、b1001 |
| B、b1002 |
| C、b2003 |
| D、不能确定的 |
在锐角△ABC中，BC=1，B=2A，则AC的取值范围为（ ）
A、（1，
| ||||
B、（
| ||||
C、（
| ||||
D、（2，
|
若|
|=6，|
|=4，
•
=-12
，则
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、120° | B、150° |
| C、135° | D、45° |