题目内容
在锐角△ABC中，BC=1，B=2A，则AC的取值范围为（ ）
A、（1，
| ||||
B、（
| ||||
C、（
| ||||
D、（2，
|
考点：正弦定理
专题：解三角形
分析：由条件可得π＞A+2A＞
，且0＜2A＜
，求得
＞A＞
．再利用正弦定理求得 AC=2cosA，再利用余弦函数的定义域和值域求得AC的取值范围．
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 6 |
解答：
解：由于在锐角△ABC中，BC=1，B=2A，故有π＞A+2A＞
，且0＜2A＜
，∴
＞A＞
．
再利用正弦定理可得
=
，即
=
，∴AC=2cosA∈（
，
），
故选：B．
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 6 |
再利用正弦定理可得
| BC |
| sinA |
| AC |
| sinB |
| 1 |
| sinA |
| AC |
| sin2A |
| 2 |
| 3 |
故选：B．
点评：本题给出锐角三角形的一个角是另一角的二倍，求边BC的取值范围，着重考查了三角形内角和定理和利用正、余弦定理解三角形等知识，属于中档题．
练习册系列答案
相关题目
半径为R的圆内接正n边形的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在圆O中，若弦AB=3，弦AC=5，则
•
的值（ ）
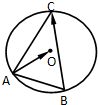
| AO |
| BC |
| A、-8 | B、-1 | C、1 | D、8 |
已知圆O：x2+y2=25，点A（-3，0）、B（3，0），一条抛物线以圆O的切线为准线且过点A和B，则这列抛物线的焦点的轨迹方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设集合M={x|f（x）=0}，N={x|g（x）=0}，则集合P={x|f（x）•g（x）=0}一定（ ）
| A、等于M∩N |
| B、等于M∪N |
| C、等于 M或N |
| D、以上都不对 |
已知△ABC中，
•
=
•
且|
+
|=|
|，则△ABC的形状为（ ）
| AB |
| BC |
| AC |
| CB |
| AC |
| AB |
| BC |
| A、锐角三角形 |
| B、钝角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
下列三视图表示的几何体是（ ）
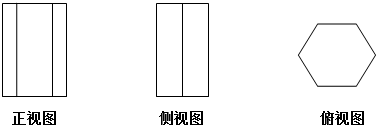
| A、正六棱柱 | B、正六棱锥 |
| C、正六棱台 | D、正六边形 |