题目内容
已知f1（x）=sinx+cosx，fn+1（x）是fn （x）的导函数，即f2（x）=f′1（x），f3（x）=f′2（x），…，fn+1（x）=f′n（x），n∈N*，则f2012（x）=（ ）
| A、sinx+cosx |
| B、sinx-cosx |
| C、-sinx+cosx |
| D、-sinx-cosx |
考点：导数的运算
专题：导数的概念及应用
分析：利用导数的运算法则，通过计算即可得出其周期性fn+4（x）=fn（x）进而即可得出答案．
解答：
解：∵f1（x）=sinx+cosx，fn+1（x）是fn（x）的导函数，
∴f2（x）=f1′（x）=cosx-sinx，f3（x）=f2′（x）=-sinx-cosx，f4（x）=-cosx+sinx，f5（x）=sinx+cosx…，
∴fn+4（x）=fn（x），
∴f2012（x）=f503×4（x）=f4（x）=sinx-cosx．
故选B．
∴f2（x）=f1′（x）=cosx-sinx，f3（x）=f2′（x）=-sinx-cosx，f4（x）=-cosx+sinx，f5（x）=sinx+cosx…，
∴fn+4（x）=fn（x），
∴f2012（x）=f503×4（x）=f4（x）=sinx-cosx．
故选B．
点评：熟练掌握导数的运算法则及得出其周期性fn+4（x）=fn（x）是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
从高一（9）班54名学生中选出5名学生参加学生代表大会，若采用下面的方法选取：先用简单随机抽样从54人中剔除4人，剩下的50人再按系统抽样的方法抽取5人，则这54人中，每人入选的概率（ ）
A、都相等，且等于
| ||
B、都相等，且等于
| ||
| C、均不相等 | ||
| D、不全相等 |
半径为R的圆内接正n边形的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个正整数数表如下（表中下一行中的数的个数是上一行中数的个数的2倍）：
则第9行中的第4个数是（ ）
| 第一行 | 1 |
| 第二行 | 2、3 |
| 第三行 | 4、5、6、7 |
| … | … |
| A、132 | B、255 |
| C、259 | D、260 |
已知集合M={0，1，2，3}，N={x|x2-3x＜0}，则M∩N=（ ）
| A、{0} |
| B、{x|x＜0} |
| C、{x|0＜x＜3} |
| D、{1，2} |
若偶函数f（x）在[-1，0]上为减函数，α，β为任意一锐角三角形的两个内角，则（ ）
| A、f（cosα）＞f（cosβ） |
| B、f（sinα）＞f（sinβ） |
| C、f（sinα）＞f（cosβ） |
| D、f（cosα）＞f（sinβ） |
如图，在圆O中，若弦AB=3，弦AC=5，则
•
的值（ ）
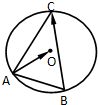
| AO |
| BC |
| A、-8 | B、-1 | C、1 | D、8 |
已知圆O：x2+y2=25，点A（-3，0）、B（3，0），一条抛物线以圆O的切线为准线且过点A和B，则这列抛物线的焦点的轨迹方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|