题目内容
观察:52-1=24,72-1=48,112-1=120,132-1=168,…所得的结果都是24的倍数,由此推测可有( )
| A、其中包含等式:152-1=224 |
| B、一般式是:(2n+3)2-1=4(n+1)(n+2) |
| C、其中包含等式1012-1=10200 |
| D、24的倍数加1必是某一质数的完全平方 |
考点:归纳推理
专题:推理和证明
分析:仔细观察每一个等式,用含有n的式子表示出等号左边的数,即可表示出24的倍数.
解答:
解:∵52-1=24,
72-1=48,
112-1=120,
132-1=168…,
即:(6×1-1)2-1=24,
(6×1+1)2-1=48,
(6×2-1)2-1=120,
(6×2+1)2-1=168,
…,
归纳可得:
∴(6n-1)2-1、(6n+1)2-1是24的倍数,
由101=6×17-1,
故推测中包含:等式1012-1=10200,
故选:C
72-1=48,
112-1=120,
132-1=168…,
即:(6×1-1)2-1=24,
(6×1+1)2-1=48,
(6×2-1)2-1=120,
(6×2+1)2-1=168,
…,
归纳可得:
∴(6n-1)2-1、(6n+1)2-1是24的倍数,
由101=6×17-1,
故推测中包含:等式1012-1=10200,
故选:C
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
复数(2+
)i的实部是( )
| 3 |
| A、2 | ||
B、
| ||
C、2+
| ||
| D、0 |
| cos85°+sin25°cos30° |
| cos25° |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、1 |
已知集合M={0,1,2,3},N={x|x2-3x<0},则M∩N=( )
| A、{0} |
| B、{x|x<0} |
| C、{x|0<x<3} |
| D、{1,2} |
要得到函数y=cos2x的图象,只需要把函数y=sin(2x+
)的图象( )
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
如图,在圆O中,若弦AB=3,弦AC=5,则
•
的值( )
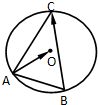
| AO |
| BC |

| A、-8 | B、-1 | C、1 | D、8 |
设 a>b,则下列不等式中恒成立的是( )
| A、a2>b2 | ||||
B、
| ||||
| C、lg(a-b)>0 | ||||
| D、2a>2b |
设集合M={x|f(x)=0},N={x|g(x)=0},则集合P={x|f(x)•g(x)=0}一定( )
| A、等于M∩N |
| B、等于M∪N |
| C、等于 M或N |
| D、以上都不对 |
 如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,ED=2
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,ED=2