题目内容
若|
|=6,|
|=4,
•
=-12
,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、120° | B、150° |
| C、135° | D、45° |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:设
与
的夹角为θ,由数量积的定义可得cosθ,可得答案.
| a |
| b |
解答:
解:设
与
的夹角为θ,则0°≤θ≤180°,
∵|
|=6,|
|=4,
•
=-12
,
∴
•
=6×4×cosθ=-12
,
解得cosθ=-
,
∴
与
的夹角θ=135°
故选:C
| a |
| b |
∵|
| a |
| b |
| a |
| b |
| 2 |
∴
| a |
| b |
| 2 |
解得cosθ=-
| ||
| 2 |
∴
| a |
| b |
故选:C
点评:本题考查数量积与向量的夹角,属基础题.

练习册系列答案
相关题目
如图,在圆O中,若弦AB=3,弦AC=5,则
•
的值( )
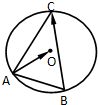
| AO |
| BC |

| A、-8 | B、-1 | C、1 | D、8 |
下列三视图表示的几何体是( )
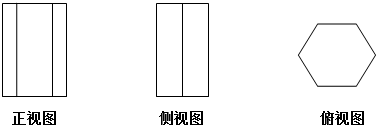

| A、正六棱柱 | B、正六棱锥 |
| C、正六棱台 | D、正六边形 |
圆ρ=
(cosθ+sinθ)的圆心坐标是( )
| 2 |
A、(
| ||||
B、(1,
| ||||
C、(
| ||||
D、(2,
|
4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,ED=2
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,ED=2