题目内容
交通管理部门为了解机动车驾驶员（简称驾驶员）对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查．假设四个社区驾驶员的总人数为N，其中甲社区有驾驶员96人．若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12，22，26，44，则这四个社区驾驶员的总人数N为（ ）
| A、104 | B、808 |
| C、832 | D、2014 |
考点：分层抽样方法
专题：概率与统计
分析：根据甲社区有驾驶员96人，在甲社区中抽取驾驶员的人数为12求出每个个体被抽到的概率，然后求出样本容量，从而求出总人数．
解答：
解：∵甲社区有驾驶员96人，在甲社区中抽取驾驶员的人数为12
∴每个个体被抽到的概率为
=
，
样本容量为12+22+26+44=104，
∴这四个社区驾驶员的总人数N为
=832．
故选：C．
∴每个个体被抽到的概率为
| 12 |
| 96 |
| 1 |
| 8 |
样本容量为12+22+26+44=104，
∴这四个社区驾驶员的总人数N为
| 104 | ||
|
故选：C．
点评：本题主要考查了分层抽样，分层抽样是最经常出现的一个抽样问题，这种题目一般出现在选择或填空中，属于基础题．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
已知直线x=0和x=
是函数f（x）=sin（ωx+φ）-
cos（ωx+φ）（ω＞0，|φ|＜
）图象的两条相邻的对称轴，则（ ）
| π |
| 2 |
| 3 |
| π |
| 2 |
A、f（x）的最小正周期为π，且在（0，
| ||||
B、f（x）的最小正周期为π，且在（0，
| ||||
C、φ=
| ||||
D、φ=
|
下列各组向量中，可以作为基底的是（ ）
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
半径为R的圆内接正n边形的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
| cos85°+sin25°cos30° |
| cos25° |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、1 |
一个正整数数表如下（表中下一行中的数的个数是上一行中数的个数的2倍）：
则第9行中的第4个数是（ ）
| 第一行 | 1 |
| 第二行 | 2、3 |
| 第三行 | 4、5、6、7 |
| … | … |
| A、132 | B、255 |
| C、259 | D、260 |
已知集合M={0，1，2，3}，N={x|x2-3x＜0}，则M∩N=（ ）
| A、{0} |
| B、{x|x＜0} |
| C、{x|0＜x＜3} |
| D、{1，2} |
如图，在圆O中，若弦AB=3，弦AC=5，则
•
的值（ ）
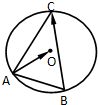
| AO |
| BC |
| A、-8 | B、-1 | C、1 | D、8 |
下列三视图表示的几何体是（ ）
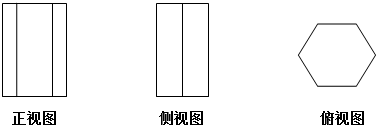
| A、正六棱柱 | B、正六棱锥 |
| C、正六棱台 | D、正六边形 |