题目内容
已知{an}是公差不为0的等差数列，且an≥0；又定义bn=
+
（1≤n≤2003 ），则{bn}的最大项是（ ）
| an |
| a2004-n |
| A、b1001 |
| B、b1002 |
| C、b2003 |
| D、不能确定的 |
考点：数列的函数特性
专题：综合题,转化思想
分析：应用数列的函数性，结合不等式放缩求解，再利用等差数列的性质即可解决．
解答：
解：因为{an}是公差不为0的等差数列，且an≥0；又定义bn=
+
所以（bn）2=（
+
）2=an+a2004-n+2
.
＜2（an+a2004-n）
an与a2004-n等差中项为第1002项，
{bn}的最大项是b1002
故选：B
| an |
| a2004-n |
所以（bn）2=（
| an |
| a2004-n |
| an |
| a2004-n |
an与a2004-n等差中项为第1002项，
{bn}的最大项是b1002
故选：B
点评：本题考查了数列的函数性，和等差数列的性质，综合运用不等式解决．
练习册系列答案
相关题目
下列各组向量中，可以作为基底的是（ ）
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知集合M={0，1，2，3}，N={x|x2-3x＜0}，则M∩N=（ ）
| A、{0} |
| B、{x|x＜0} |
| C、{x|0＜x＜3} |
| D、{1，2} |
如图，在圆O中，若弦AB=3，弦AC=5，则
•
的值（ ）
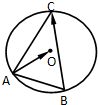
| AO |
| BC |
| A、-8 | B、-1 | C、1 | D、8 |
设 a＞b，则下列不等式中恒成立的是（ ）
| A、a2＞b2 | ||||
B、
| ||||
| C、lg（a-b）＞0 | ||||
| D、2a＞2b |
已知圆O：x2+y2=25，点A（-3，0）、B（3，0），一条抛物线以圆O的切线为准线且过点A和B，则这列抛物线的焦点的轨迹方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设集合M={x|f（x）=0}，N={x|g（x）=0}，则集合P={x|f（x）•g（x）=0}一定（ ）
| A、等于M∩N |
| B、等于M∪N |
| C、等于 M或N |
| D、以上都不对 |
下列三视图表示的几何体是（ ）
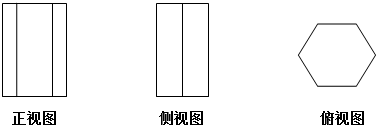
| A、正六棱柱 | B、正六棱锥 |
| C、正六棱台 | D、正六边形 |