题目内容
已知圆C的圆心为直线x-y+1=0与2x+y-4=0的交点,且圆C与直线3x+4y+14=0相切.
(1)求圆C的标准方程;
(2)过点P(-1,-2)作直线l,①证明:直线l与圆C恒相交;②求直线l被圆截得的弦长最短时的方程.
(1)求圆C的标准方程;
(2)过点P(-1,-2)作直线l,①证明:直线l与圆C恒相交;②求直线l被圆截得的弦长最短时的方程.
考点:圆的标准方程,直线与圆的位置关系
专题:直线与圆
分析:(1)求出圆的圆心坐标,利用圆心到直线的距离求出半径,即可求圆C的标准方程;
(2)过点P(-1,-2)作直线l,①通过点与圆心的距离与半径比较即可证明:直线l与圆C恒相交;
②利用圆心距,半径,想的关系,即可求直线l被圆截得的弦长最短时的方程.
(2)过点P(-1,-2)作直线l,①通过点与圆心的距离与半径比较即可证明:直线l与圆C恒相交;
②利用圆心距,半径,想的关系,即可求直线l被圆截得的弦长最短时的方程.
解答:
(满分12分)
解:(1)联立
得圆心为(1,2)
因为直线与圆相切,所以r=
=5
所以圆C的标准方程为(x-1)2+(y-2)2=25---------------------------------(4分)
(2)①|PC|=2
<5所以点P在圆内,
所以过圆内一点作直线l与圆C恒相交------------------------(7分)
②l被圆截得的弦长最短,则圆心到直线的距离最大,此时PC⊥l----------(8分)
直线PC的斜率为2,所以直线l的斜率为-
--------------------------(10分)
l的方程为x+2y+5=0----------------------------------------(12分)
解:(1)联立
|
因为直线与圆相切,所以r=
| |3+8+14| |
| 5 |
所以圆C的标准方程为(x-1)2+(y-2)2=25---------------------------------(4分)
(2)①|PC|=2
| 5 |
所以过圆内一点作直线l与圆C恒相交------------------------(7分)
②l被圆截得的弦长最短,则圆心到直线的距离最大,此时PC⊥l----------(8分)
直线PC的斜率为2,所以直线l的斜率为-
| 1 |
| 2 |
l的方程为x+2y+5=0----------------------------------------(12分)
点评:本题考查圆的方程的求法,点与圆的位置关系,直线与圆的位置关系的应用,基本知识的考查.

练习册系列答案
相关题目
已知f(x)=kx+b(k<0),且f[f(x)]=4x+1,则f(x)=( )
| A、-2x-1 | ||
| B、-2x+1 | ||
| C、-x+1 | ||
D、-2x-
|
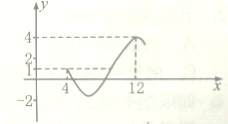 如图为函数f(x)=Asin(ωx+φ)+C(A>0,ω>0,0<φ<π)图象的一部分.
如图为函数f(x)=Asin(ωx+φ)+C(A>0,ω>0,0<φ<π)图象的一部分.