题目内容
若a＞0，且a≠1，则函数y=ax-1+1的图象一定过定点 ．
考点：指数函数的图像与性质
专题：函数的性质及应用
分析：令a的幂指数x-1=0，可得 x=1，此时求得y=2，由此可得所求的定点坐标．
解答：
解：令a的幂指数x-1=0，可得 x=1，此时求得y=2，故所求的定点坐标为（1，2），
故答案为 （1，2）．
故答案为 （1，2）．
点评：本题主要考查指数函数的单调性和特殊点，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
若sin（π+α）=
，α是第三象限的角，则
=（ ）
| 3 |
| 5 |
sin
| ||||
sin
|
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
已知集合A={x|x≥2014}，B={x|x≥2015}，则集合A∪B=（ ）
| A、{x|x≥2014} |
| B、{x|x≥2015} |
| C、{x|2014≤x≤2015} |
| D、{x|x≤2014或x≥2015} |
已知集合A={x||x|＜2}，B={x|x2＞1}，则A∩B=（ ）
| A、（1，2） |
| B、（-2，-1） |
| C、（-2，-1）∪（1，2） |
| D、∅ |
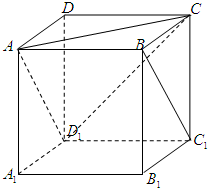如图，正方体ABCD-A1B1C1D1，则下列四个命题：