Question

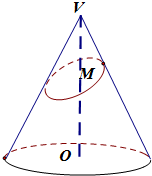如图，已知圆锥底半径为1，高VO=2，过VO的中点M作一个与圆锥底面成θ角且tanθ=3的平面，得到截口曲线．数学家Germinal Dandelin已经证明该曲线是椭圆，求此椭圆的离心率．

Answer 1

考点：椭圆的简单性质

专题：计算题,圆锥曲线的定义、性质与方程

分析：可作椭圆面在底面上的射影，即为圆面，设半径为r，由于椭圆面与圆面所成的角为θ，则有∠MAB=θ，设AM=a，则有2acosθ=2r，再由tanθ=3，求得cosθ，解得a，再由b=r，求出c，运用离心率公式，即可得到．

解答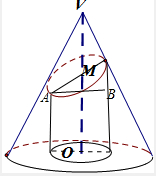： 解：过VO的中点M作一个与圆锥底面成θ角且tanθ=3的平面，
其截口是一个椭圆，
可作椭圆面在底面上的射影，即为圆面，
设半径为r，由于椭圆面与圆面所成的角为θ，
则有∠MAB=θ，设AM=a，则有2acosθ=2r，又tanθ=3，
由

sinθ

cosθ

=3，sin²θ+cos²θ=1，得cosθ=

1

10

，
即有a=

10

r，又b=r，则c=

a2-b2

=3r，
则离心率为e=

c

a

=

3 10

10

．

点评：本题考查椭圆的离心率的求法，注意转化思想，确定椭圆的a，b是解题的关键，属于中档题．