题目内容
已知函数x、y满足约束条件
.
(1)若z=x2+y2,求z的最小值和最大值;
(2)若z=
,求z的最小值和最大值.
|
(1)若z=x2+y2,求z的最小值和最大值;
(2)若z=
| y-2 |
| x+1 |
考点:简单线性规划
专题:直线与圆
分析:由已知条件作出可行域,利用角点法能求出z的最小值和最大值.
解答:
解:(1)∵函数x、y满足约束条件
,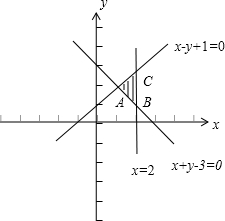
∴作出如图所示的可行域,可行域为△ABC,
解方程组
,得A(1,2),
解方程组
,得B(2,1),
解方程组
,得C(2,3),
∵z=x2+y2,
∴ZA=12+22=5,
ZB=22+12=5,
ZC=22+32=13,
∴z的最小值为5,最大值为13.
(2)∵z=
,
∴ZA=
=0,
ZB=
=-
,
ZC=
=
,
∴z的最小值为-
,最大值为
.
|

∴作出如图所示的可行域,可行域为△ABC,
解方程组
|
解方程组
|
解方程组
|
∵z=x2+y2,
∴ZA=12+22=5,
ZB=22+12=5,
ZC=22+32=13,
∴z的最小值为5,最大值为13.
(2)∵z=
| y-2 |
| x+1 |
∴ZA=
| 2-2 |
| 1+1 |
ZB=
| 1-2 |
| 2+1 |
| 1 |
| 3 |
ZC=
| 3-2 |
| 2+1 |
| 1 |
| 3 |
∴z的最小值为-
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查函数的最大值和最小值的求法,是中档题,解题时要注意角点法的合理运用.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
集合A={x|y=log2(1-x)},B={x|x2>0},则A∩B=( )
| A、(0,1) |
| B、(0,1] |
| C、(-∞,1) |
| D、(-∞,0)∪(0,1) |
下列指定的对象,不能够构成集合的是( )
| A、一年中有31天的月份 |
| B、平面上到点O距离是1的点 |
| C、满足方程x2-2x-3=0的x |
| D、某校高一(1)班性格开朗的女生 |
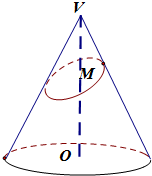 如图,已知圆锥底半径为1,高VO=2,过VO的中点M作一个与圆锥底面成θ角且tanθ=3的平面,得到截口曲线.数学家Germinal Dandelin已经证明该曲线是椭圆,求此椭圆的离心率.
如图,已知圆锥底半径为1,高VO=2,过VO的中点M作一个与圆锥底面成θ角且tanθ=3的平面,得到截口曲线.数学家Germinal Dandelin已经证明该曲线是椭圆,求此椭圆的离心率.