题目内容
已知椭圆中心在坐标原点，焦点在x轴上，短轴长小于焦距长．以其两个焦点和短轴的两个端点为顶点的
四边形是一个内角为120°且面积为2
的菱形，设P为该椭圆上的动点，C、D的坐标分别是（-
，0），
（
，0），则PC•PD的最大值为 ．
四边形是一个内角为120°且面积为2
| 3 |
| 3 |
（
| 3 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：利用菱形的面积求出椭圆的焦距、长轴长；利用椭圆的定义求出P到两焦点的距离，利用基本不等式求出最值．
解答：
解：据题意，a=2b，c=
b，
2
b2=2
，
解得b2=1，
∴a2=4，c=
，
∴C，D为焦点，
∴|PC|+|PD|=2a=4，
∴|PC||PD|≤(
)2=4．
故答案为：4．
| 3 |
2
| 3 |
| 3 |
解得b2=1，
∴a2=4，c=
| 3 |
∴C，D为焦点，
∴|PC|+|PD|=2a=4，
∴|PC||PD|≤(
| |PC|+|PD| |
| 2 |
故答案为：4．
点评：本题考查椭圆的定义、等价转化的能力、基本不等式，考查运算能力，属中档题．
练习册系列答案
相关题目
下列指定的对象，不能够构成集合的是（ ）
| A、一年中有31天的月份 |
| B、平面上到点O距离是1的点 |
| C、满足方程x2-2x-3=0的x |
| D、某校高一（1）班性格开朗的女生 |
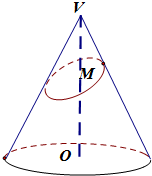如图，已知圆锥底半径为1，高VO=2，过VO的中点M作一个与圆锥底面成θ角且tanθ=3的平面，得到截口曲线．数学家Germinal Dandelin已经证明该曲线是椭圆，求此椭圆的离心率．