题目内容
已知斜三棱柱ABC-A1B1C1的棱长都是a,侧棱与底面所成角为60°,侧面BB1C1C⊥底面ABC,求该三棱柱体积.
考点:棱柱、棱锥、棱台的体积
专题:计算题,作图题,空间位置关系与距离
分析:分析可知,作B1D⊥BC于点D,则B1D是该三棱柱的高,由题意求出高和底面面积,从而求出体积.
解答:
解:如右图,作B1D⊥BC于点D,
∵侧面BB1C1C⊥底面ABC,侧面BB1C1C∩底面ABC=BC,
∴B1D⊥平面ABC,
则B1D是该三棱柱的高,
B1D=BB1×sin60°=
a,
底面ABC的面积为S=
×a×a×sin60°=
a2,
则该三棱柱体积V=
×S×B1D
=
×
a2×
a=
.

∵侧面BB1C1C⊥底面ABC,侧面BB1C1C∩底面ABC=BC,
∴B1D⊥平面ABC,
则B1D是该三棱柱的高,
B1D=BB1×sin60°=
| ||
| 2 |
底面ABC的面积为S=
| 1 |
| 2 |
| ||
| 4 |
则该三棱柱体积V=
| 1 |
| 3 |
=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 2 |
| a3 |
| 8 |
点评:本题考查了学生的空间想象力及作图的能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
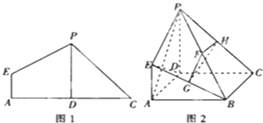 如图1,在平面四边形ACPE中,D为AC中点,AD=DC=PD=2,AE=1,且AE⊥AC,PD⊥AC,现沿PD折起使∠ADC=90°,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
如图1,在平面四边形ACPE中,D为AC中点,AD=DC=PD=2,AE=1,且AE⊥AC,PD⊥AC,现沿PD折起使∠ADC=90°,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点. 已知函数f(x)=
已知函数f(x)=