题目内容
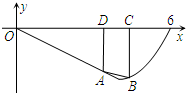 已知函数f(x)=
已知函数f(x)=
|
考点:分段函数的应用,函数解析式的求解及常用方法
专题:计算题,函数的性质及应用
分析:分别求0<t≤3,3<t<4,4≤t<5,面积S的表达式,注意运用f(x)的表达式和梯形面积公式,再求各段的最大值,注意运用配方和二次函数的性质,再求最大的即可.
解答:
解:当t>0且t+1≤4时,即0<t≤3,
AD=|f(t)|=
t,BC=|f(t+1)|=
(t+1),CD=1,
则S=
=
t+
,
当t<4且t+1>4,即3<t<4,
AD=
t,BC=|f(t+1)|=-
(t+1)2+4(t+1)-6,
则S=
=-
t2+
t-
,
当t≥4且t+1<6即4≤t<5,
AD=|f(t)|=-
t2+4t-6,BC=|f(t+1)|=-
(t+1)2+4(t+1)-6,
则S=
=-
t2+
t-
,
∴S=
,
当0<t≤3时,Smax=
×3+
=
;
当3<t<4时,S=-
(t-
)2+
,t=
,得Smax=
;
当4≤t<5时,S=-
(t-
)2+
,t=4,得Smax=
.
综上,t=
,得S取最大值,且为
.
AD=|f(t)|=
| 1 |
| 2 |
| 1 |
| 2 |
则S=
| (AD+BC)•CD |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
当t<4且t+1>4,即3<t<4,
AD=
| 1 |
| 2 |
| 1 |
| 2 |
则S=
| (AD+BC)•CD |
| 2 |
| 1 |
| 4 |
| 7 |
| 4 |
| 5 |
| 4 |
当t≥4且t+1<6即4≤t<5,
AD=|f(t)|=-
| 1 |
| 2 |
| 1 |
| 2 |
则S=
| (AD+BC)•CD |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 17 |
| 4 |
∴S=
|
当0<t≤3时,Smax=
| 1 |
| 2 |
| 1 |
| 4 |
| 7 |
| 4 |
当3<t<4时,S=-
| 1 |
| 4 |
| 7 |
| 2 |
| 29 |
| 16 |
| 7 |
| 2 |
| 29 |
| 16 |
当4≤t<5时,S=-
| 1 |
| 2 |
| 7 |
| 2 |
| 15 |
| 8 |
| 7 |
| 4 |
综上,t=
| 7 |
| 2 |
| 29 |
| 16 |
点评:本题考查分段函数的运用,求分段函数表达式,考查分段函数的最值,注意对各段分别求最值,再求最大的,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
已知集合A={-1,0,1},B={-1,0},则A∩B=( )
| A、{-1} |
| B、{0} |
| C、{-1,0} |
| D、{-1,0,1} |