题目内容
已知函数f(x)=ln(x+
)-ax,其中a∈R且a≠0.
(1)讨论f(x)的单调性;
(2)若不等式f(x)<ax恒成立,求实数a取值范围;
(3)若方程f(x)=0存在两个异号实根x1,x2,求证:x1+x2>0.
| 1 |
| a |
(1)讨论f(x)的单调性;
(2)若不等式f(x)<ax恒成立,求实数a取值范围;
(3)若方程f(x)=0存在两个异号实根x1,x2,求证:x1+x2>0.
考点:利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)先求导数,研究导函数的函数值,通过导数大于0从而确定出函数f(x)的单调递增区间即可,求单调递增区间必须注意函数的定义域.
(2)若任意x∈[0,+∞),f(x)≤x恒成立,则必有x≥0时,即要求函数则h(x)=2ax-ln(x+
)的最大值小于等于0即可.
(3)设g(x)=f(-x)-f(x)则∴g′(x)=
,然后利用单调性,问题得以证明.
(2)若任意x∈[0,+∞),f(x)≤x恒成立,则必有x≥0时,即要求函数则h(x)=2ax-ln(x+
| 1 |
| a |
(3)设g(x)=f(-x)-f(x)则∴g′(x)=
| 2ax2 | ||
x2-
|
解答:
解:(1)f(x)定义域为(-
,+∞),
其导数f′(x)=-
,
①当a<0时,f′(x)>0,函数f(x)在(-
,+∞)上是增函数;
②当a>0时,在区间(-
,0)上,f′(x)>0;在区间(0,+∞)上,f′(x)<0,
∴f(x)在区间(-
,0)上是增函数,在(0,+∞)是减函数;
(2)当a<0时,则x取适当的数能使f(x)≥ax,比如取x=e-
,
能使f(e-
)=1-a(e-
)=2-ae>ae-1=a(e-
),
∴a<0不合题意,
当a>0时,令h(x)=ax-f(x),则h(x)=2ax-ln(x+
),
问题化为求h(x)>0恒成立时a的取值范围.
由于h′(x)=2a-
=
,
∴在区间(-
,-
)上,h′(x)<0;在区间(-
,+∞)上,h′(x)>0,
∴h(x)的最小值为h(-
),所以只需h(-
)>0,
即2a-(-
)-ln((-
+
)>0,∴ln
<-1,∴a>
;
(3)由于f(x)=0存在两个异号实根x1,x2,不仿设x1<0,-
<x1<0,a>0,
造函数:g(x)=f(-x)-f(x),-
<x<0,
∴g(x)=ln(
-x)-ln(x+
)+2ax,
∴g′(x)=
<0,
∴g(x)在-
<x<0,为减函数,又-
<x1<0,
∴g(x1)>g(0)=0,
∴f(-x)-f(x)>0,f(x1)=0,
∵f(-x1)>0=f(x2),
∴x1+x2>0.
| 1 |
| a |
其导数f′(x)=-
| a2x |
| ax+1 |
①当a<0时,f′(x)>0,函数f(x)在(-
| 1 |
| a |
②当a>0时,在区间(-
| 1 |
| a |
∴f(x)在区间(-
| 1 |
| a |
(2)当a<0时,则x取适当的数能使f(x)≥ax,比如取x=e-
| 1 |
| a |
能使f(e-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
∴a<0不合题意,
当a>0时,令h(x)=ax-f(x),则h(x)=2ax-ln(x+
| 1 |
| a |
问题化为求h(x)>0恒成立时a的取值范围.
由于h′(x)=2a-
| 1 | ||
x+
|
2a(x+
| ||
x+
|
∴在区间(-
| 1 |
| a |
| 1 |
| 2a |
| 1 |
| 2a |
∴h(x)的最小值为h(-
| 1 |
| 2a |
| 1 |
| 2a |
即2a-(-
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| a |
| 1 |
| 2a |
| e |
| 2 |
(3)由于f(x)=0存在两个异号实根x1,x2,不仿设x1<0,-
| 1 |
| a |
造函数:g(x)=f(-x)-f(x),-
| 1 |
| a |
∴g(x)=ln(
| 1 |
| a |
| 1 |
| a |
∴g′(x)=
| 2ax2 | ||
x2-
|
∴g(x)在-
| 1 |
| a |
| 1 |
| a |
∴g(x1)>g(0)=0,
∴f(-x)-f(x)>0,f(x1)=0,
∵f(-x1)>0=f(x2),
∴x1+x2>0.
点评:本题考查利用导数研究函数的极值以及由函数恒成立的问题求参数的取值范围,求解本题关键是记忆好求导的公式以及极值的定义,对于函数的恒成立的问题求参数,要注意正确转化,恰当的转化可以大大降低解题难度.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
设命题p:平面α∩平面β=l,若m⊥l,则m⊥β;命题q:函数y=cos(x-
)的图象关于直线x=
对称.则下列判断正确的是( )
| π |
| 2 |
| π |
| 2 |
| A、p为真 | B、¬q为假 |
| C、p∨q为假 | D、p∧q为真 |
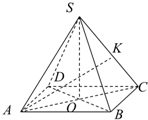 如图,设S-ABCD是一个高为3的四棱锥,底面ABCD是边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心.K是棱SC的中点.试求直线AK与平面SBC所成角的大小.
如图,设S-ABCD是一个高为3的四棱锥,底面ABCD是边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心.K是棱SC的中点.试求直线AK与平面SBC所成角的大小.