题目内容
已知曲线C:y2=2x-4.
(1)求曲线C在点A(3,
)处的切线方程;
(2)过原点O作直线l与曲线C交于A,B两不同点,求线段AB的中点M的轨迹方程.
(1)求曲线C在点A(3,
| 2 |
(2)过原点O作直线l与曲线C交于A,B两不同点,求线段AB的中点M的轨迹方程.
考点:轨迹方程,利用导数研究曲线上某点切线方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)y>0时,y=
,求导数,可得切线的斜率,从而可求曲线C在点A(3,
)处的切线方程;
(2)设l:y=kx代入y2=2x-4,利用韦达定理,结合中点坐标公式,即可求出线段AB的中点M的轨迹方程.
| 2x-4 |
| 2 |
(2)设l:y=kx代入y2=2x-4,利用韦达定理,结合中点坐标公式,即可求出线段AB的中点M的轨迹方程.
解答:
解:(1)y>0时,y=
,
∴y′=
,
∴x=3时,y′=
,
∴曲线C在点A(3,
)处的切线方程为y-
=
(x-3),即x-
y-1=0;
(2)设l:y=kx,M(x,y),则
y=kx代入y2=2x-4,可得k2x2-2x+4=0,
∴△=4-16k2>0,∴
>2
设A(x1,y1)、B(x2,y2),则x1+x2=
,
∴y1+y2=
∴x=
,y=
,
∴y2=x(x>4).
| 2x-4 |
∴y′=
| 1 | ||
|
∴x=3时,y′=
| ||
| 2 |
∴曲线C在点A(3,
| 2 |
| 2 |
| ||
| 2 |
| 2 |
(2)设l:y=kx,M(x,y),则
y=kx代入y2=2x-4,可得k2x2-2x+4=0,
∴△=4-16k2>0,∴
| 1 |
| 2k2 |
设A(x1,y1)、B(x2,y2),则x1+x2=
| 2 |
| k2 |
∴y1+y2=
| 2 |
| k |
∴x=
| 1 |
| k2 |
| 1 |
| k |
∴y2=x(x>4).
点评:本题考查导数的几何意义,考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生的计算能力,正确运用韦达定理是关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
若sinα+cosα=
(0<α<π),则tanα=( )
| 7 |
| 13 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
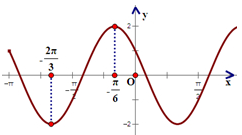 如图所示为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象.
如图所示为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象. 函数y=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的图象如图所示,则该函数的解析式为y=
函数y=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的图象如图所示,则该函数的解析式为y=