题目内容
设命题p:平面α∩平面β=l,若m⊥l,则m⊥β;命题q:函数y=cos(x-
)的图象关于直线x=
对称.则下列判断正确的是( )
| π |
| 2 |
| π |
| 2 |
| A、p为真 | B、¬q为假 |
| C、p∨q为假 | D、p∧q为真 |
考点:复合命题的真假
专题:简易逻辑
分析:首先,判断命题p和命题q的真假,然后,结合复合命题的真假情况进行判断.
解答:
解:由命题p:
∵m⊥l,
∴m∥β或m⊥β或m?β,
∴命题p为假命题;
由命题q得:
y=cos(x-
)=cos(
-x)=sinx,
∴y=sinx的图象关于直线x=
对称.
∴命题q为真命题;
∴命题¬q为假命题;
故选B.
∵m⊥l,
∴m∥β或m⊥β或m?β,
∴命题p为假命题;
由命题q得:
y=cos(x-
| π |
| 2 |
| π |
| 2 |
∴y=sinx的图象关于直线x=
| π |
| 2 |
∴命题q为真命题;
∴命题¬q为假命题;
故选B.
点评:本题重点考查命题的真假判断,复合命题的真值表的应用,属于基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
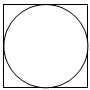 一次实验:向如图所示的正方形中随机撒一大把豆子,经查数,落在正方形中的豆子的总数为N粒,其中m(m<N)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )
一次实验:向如图所示的正方形中随机撒一大把豆子,经查数,落在正方形中的豆子的总数为N粒,其中m(m<N)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )A、
| ||
B、
| ||
C、
| ||
D、
|
下列等式中,成立的是( )
A、sin(
| ||||
| B、sin(x+2π)=sinx | ||||
| C、sin(2π+x)=-sinx | ||||
| D、cos(π+x)=cosx |
在复平面内,复数i(2+3i)对应点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
将函数y=sin2x的图象向右平移
个单位,得到y=cos(2x+φ),φ∈(-π,π]的图象,则φ的值为( )
| π |
| 6 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知正三角形ABC的顶点A(
,1),B(3
,1),顶点C在第一象限,若点M(x,y)在△ABC的内部或边界,则z=
•
取最大值时,3x2+y2有( )
| 3 |
| 3 |
| OA |
| OM |
| A、定值52 | B、定值82 |
| C、最小值52 | D、最小值50 |
若sinα+cosα=
(0<α<π),则tanα=( )
| 7 |
| 13 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|