题目内容
已知一次函数f（x）满足f（f（x））=4x+3，求f（x）的解析式．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：设一次函数f（x）=ax+b，代入已知比较系数可得a和b的方程组，解方程组可得．
解答：
解：设一次函数f（x）=ax+b，
则f（f（x））=a（ax+b）+b
=a2x+ab+b=4x+3，
∴
，
得
或
，
∴f（x）=2x+1，或f（x）=-2x-3
则f（f（x））=a（ax+b）+b
=a2x+ab+b=4x+3，
∴
|
得
|
|
∴f（x）=2x+1，或f（x）=-2x-3
点评：本题考查待定系数法求函数的解析式，涉及方程组的解法，属中档题．
练习册系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
下列等式中，成立的是（ ）
A、sin（
| ||||
| B、sin（x+2π）=sinx | ||||
| C、sin（2π+x）=-sinx | ||||
| D、cos（π+x）=cosx |
若sinα+cosα=
(0＜α＜π)，则tanα=（ ）
| 7 |
| 13 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
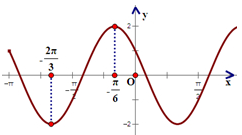如图所示为函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象．