题目内容

解下列不等式：
（1）ax2+2ax+4≤0；
（2）（a-2）x2-（4a-3）x+（4a+2）≥0．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：（1）通过对a和△分类讨论，利用一元二次不等式的解法即可解出；
（2）通过对a分类讨论，利用一元二次不等式的解法即可得出．
解答： 解：（1）①当a=0时，原不等式可化为4≤0，不成立，应舍去．
②当a≠0时，△=4a2-16a．
当a=4时，△=0，原不等式可化为（x+1）2≤0，解得x=-1，此时原不等式的解集为{-1}；
当△＜0时，解得0＜a＜4．此时原不等式的解集为∅．
当△＞0时，解得a＞4或a＜0．由ax2+2ax+4=0，解得x=
-2a±2
a2-4a
2a
=
-a±
a2-4a
a
，
当a＞4时，原不等式的解集为{x|
-a-
a2-4a
a
≤x≤
-a+
a2-4a
a
}；
当a＜0时，原不等式的解集为{x|x≥
-a-
a2-4a
a
或x≤
-a+
a2-4a
a
}．
综上可得：当a=4时，不等式的解集为{-1}；
当△＜0时，不等式的解集为∅．
当△＞0时，当a＞4时，不等式的解集为{x|
-a-
a2-4a
a
≤x≤
-a+
a2-4a
a
}；
当a＜0时，不等式的解集为{x|x≥
-a-
a2-4a
a
或x≤
-a+
a2-4a
a
}．
（2）①当a=2时，原不等式化为-5x+10≥0，解得x≤2，此时不等式的解集为{x|x≤2}；
②当a≠2时，△=25．此时不等式化为[（a-2）x-（2a+1）]（x-2）≥0，
当a＞2时，化为(x-
2a+1
a-2
)(x-2)≥0，此时
2a+1
a-2
＞2，
因此不等式的解集为{x|x≥
2a+1
a-2
或x≤2}；
当a＜2时，
2a+1
a-2
＜2，此时不等式化为(x-
2a+1
a-2
)(x-2)≤0，不等式的解集为{x|
2a+1
a-2
≤x≤2}．
综上可得：①当a=2时，不等式的解集为{x|x≤2}；
②当a＞2时，不等式的解集为{x|x≥
2a+1
a-2
或x≤2}；
当a＜2时，不等式的解集为{x|
2a+1
a-2
≤x≤2}．
点评：本题考查了分类讨论、一元二次不等式的解法，考查了计算能力，属于难题．
练习册系列答案
相关题目
在复平面内，复数i（2+3i）对应点位于（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1，F2，右顶点为A，直线l过F2交椭圆于B，C两点．
（1）如果直线l的方程为y=x-1，且△F1BC为直角三角形，求椭圆方程；
（2）证明：以A为圆心，半径为b的圆上任意一点到F1，F2的距离之比为定值．
已知sinx+cosx=
5
13
2
，且x∈（
π
4
，
3π
4
）．
（1）求cosx；
（2）求
1-tanx
1+tanx
．
已知函数f（x）=|x-a|-
9
x
+a，x∈[1，6]，a∈R．
（1）若a=1，试判断并用定义证明函数f（x）的单调性；
（2）当a∈（1，6）时，求函数f（x）的最大值的表达式M（a）．
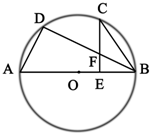如图：AB是⊙O的直径，C是弧BD的中点，CE⊥AB，垂足为E，BD交CE于点F．
（Ⅰ）求证：CF=BF；
（Ⅱ）若AD=4，⊙O的半径为6，求BC的长．
已知函数f（x）=ln（x+
1
a
）-ax，其中a∈R且a≠0．
（1）讨论f（x）的单调性；
（2）若不等式f（x）＜ax恒成立，求实数a取值范围；
（3）若方程f（x）=0存在两个异号实根x1，x2，求证：x1+x2＞0．
设x∈（0，
π
2
），求
sin2xcos2x+2
sin2xcos2x-2
的最小值．
命题“?x∈R，
x2+9
＞3”的否定是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网