题目内容
解不等式：-1＜
≤3．
| x |
| 2x-1 |
考点：其他不等式的解法
专题：不等式的解法及应用
分析：将不等式转化为不等式组，即可得到结论．
解答：
解：①若2x-1＞0，则不等式等价为-2x+1＜x≤3（2x-1），
即
，即
，解得x≥
．
②若2x-1＜0，则不等式等价为-2x+1＞x≥3（2x-1），
即
，即
，解得x＜
．
综上不等式的解集为{x|x≥
或x＜
}．
即
|
|
| 3 |
| 5 |
②若2x-1＜0，则不等式等价为-2x+1＞x≥3（2x-1），
即
|
|
| 1 |
| 3 |
综上不等式的解集为{x|x≥
| 3 |
| 5 |
| 1 |
| 3 |
点评：本题主要考查不等式的解法，利用分式不等式的解法，注意讨论分母的符号．
练习册系列答案
相关题目
已知正三角形ABC的顶点A（
，1），B（3
，1），顶点C在第一象限，若点M（x，y）在△ABC的内部或边界，则z=
•
取最大值时，3x2+y2有（ ）
| 3 |
| 3 |
| OA |
| OM |
| A、定值52 | B、定值82 |
| C、最小值52 | D、最小值50 |
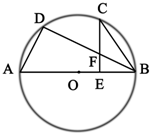如图：AB是⊙O的直径，C是弧BD的中点，CE⊥AB，垂足为E，BD交CE于点F．