题目内容
将函数y=2x2进行平移,使得到的图形与抛物线y=-2x2+4x+2的两个交点关于原点对称,求平移后的函数解析式.
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:设平移向量为
=(h,k),可得函数解析式为y=2(x-h)2+k,设M(m,n)和M′(-m,-n)是y=-2x2+4x+2与y=2(x-h)2+k的两个交点,由点在已知函数解析式可得m、n的值,再由点在要求函数图象可得h、k的方程组,解方程组可得函数解析式.
| a |
解答:
解:设平移向量为
=(h,k),则将y=2x2平移之后得到的图象的解析式为y=2(x-h)2+k,
设M(m,n)和M′(-m,-n)是y=-2x2+4x+2与y=2(x-h)2+k的两个交点,
则
,解得:
或
,
∴点(1,4)和点(-1,-4)在函数y=2(x-h)2+k的图象上,
∴
,解得
故所求解析式为:y=2(x+1)2-4,即y=2x2+4x-2.
| a |
设M(m,n)和M′(-m,-n)是y=-2x2+4x+2与y=2(x-h)2+k的两个交点,
则
|
|
|
∴点(1,4)和点(-1,-4)在函数y=2(x-h)2+k的图象上,
∴
|
|
故所求解析式为:y=2(x+1)2-4,即y=2x2+4x-2.
点评:本题考查函数解析式的求解,涉及函数图象的平移,属基础题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
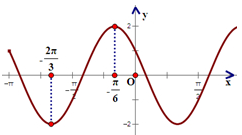 如图所示为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象.
如图所示为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象.