题目内容
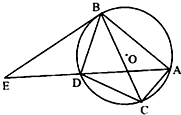（A）如图，△ABC内接圆O，AD平分∠BAC交圆于点D，过点B作圆O的切线交直线AD于点E．（Ⅰ）求证：∠EBD=∠CBD
（Ⅱ）求证：AB•BE=AE•DC．
考点：与圆有关的比例线段
专题：综合题,立体几何
分析：（Ⅰ）根据BE为圆O的切线，证明∠EBD=∠BAD，AD平分∠BAC，证明∠BAD=∠CAD，即可证明∠EBD=∠CBD
（Ⅱ）证明△EBD∽△EAB，可得AB•BE=AE•BD，利用AD平分∠BAC，即可证明AB•BE=AE•DC．
（Ⅱ）证明△EBD∽△EAB，可得AB•BE=AE•BD，利用AD平分∠BAC，即可证明AB•BE=AE•DC．
解答：
证明：（Ⅰ）∵BE为圆O的切线，
∴∠EBD=∠BAD，
∵AD平分∠BAC，
∴∠BAD=∠CAD，
∴∠EBD=∠CAD，
∵∠CBD=∠CAD，
∴∠EBD=∠CBD；
（Ⅱ）在△EBD和△EAB中，∠E=∠E，∠EBD=∠EAB，
∴△EBD∽△EAB，
∴
=
，
∴AB•BE=AE•BD，
∵AD平分∠BAC，
∴BD=DC，
∴AB•BE=AE•DC．
∴∠EBD=∠BAD，
∵AD平分∠BAC，
∴∠BAD=∠CAD，
∴∠EBD=∠CAD，
∵∠CBD=∠CAD，
∴∠EBD=∠CBD；
（Ⅱ）在△EBD和△EAB中，∠E=∠E，∠EBD=∠EAB，
∴△EBD∽△EAB，
∴
| BE |
| AE |
| BD |
| AB |
∴AB•BE=AE•BD，
∵AD平分∠BAC，
∴BD=DC，
∴AB•BE=AE•DC．
点评：本题考查弦切角定理，考查三角形的相似，考查角平分线的性质，属于中档题．
练习册系列答案
相关题目
sin61°cos31°-cos61°sin31°=（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
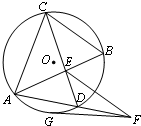如图，E是圆O内两弦AB和CD的交点，过AD延长线上一点F作圆O的切线FG，G为切点，已知EF=FG．求证：