题目内容
设抛物线y2=8x的焦点F,准线为l,P为抛物线上一点,PA⊥l,A为垂足,如果|PF|=8,则直线AF的斜率为 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据抛物线的性质求得|PA|的值,进而求得P的横坐标,代入抛物线方程求得P的纵坐标,根据抛物线方程求得F的坐标,最后利用直线斜率公式求得直线AF的斜率.
解答:
解:∵依据抛物线的性质|PA|=|PF|,
∴|PA|=8,
∵抛物线y2=8x,2P=8,
∴P=4,F的坐标(2,0)
∴xP=8-
=6,
∴yP=±
=±4
,
∴直线AF的斜率为
=±
.
故答案为:±
.
∴|PA|=8,
∵抛物线y2=8x,2P=8,
∴P=4,F的坐标(2,0)
∴xP=8-
| P |
| 2 |
∴yP=±
| 8×6 |
| 3 |
∴直线AF的斜率为
±4
| ||
| 6-2 |
| 3 |
故答案为:±
| 3 |
点评:本题主要考查了抛物线的简单性质.解题的时候一定注意有两个解.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
已知sin(π+α)=
sin(
-α),且α∈(-π,0),则α=( )
| 3 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知i为虚数单位,若(1+i)(2-i)=a+i,则实数a的值为( )
| A、-1 | B、1 | C、-3 | D、3 |

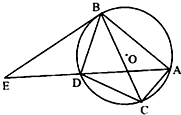 (A)如图,△ABC内接圆O,AD平分∠BAC交圆于点D,过点B作圆O的切线交直线AD于点E.
(A)如图,△ABC内接圆O,AD平分∠BAC交圆于点D,过点B作圆O的切线交直线AD于点E.