题目内容
11.已知“x>k”是“$\frac{3}{|x|}$<1”的充分不必要条件,则k的取值范围是( )| A. | [3,+∞) | B. | [2,+∞) | C. | (3,+∞) | D. | (一∞,-3] |
分析 根据充分条件和必要条件的定义结合不等式的关系进行转化求解即可.
解答 解:由$\frac{3}{|x|}$<1得|x|>3,得x>3或x<-3,
若“x>k”是“$\frac{3}{|x|}$<1”的充分不必要条件,
则k≥3,
则实数k的取值范围是[3,+∞),
故选:A
点评 本题主要考查充分条件和必要条件的应用,根据不等式的关系进行转化是解决本题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
1.点P(2,4)关于直线x+y+1=0的对称点的坐标为( )
| A. | (5,-3) | B. | (3,-5) | C. | (-5,3) | D. | (-5,-3) |
2.已知命题p:?x∈R,log2(3x+1)≤0,则( )
| A. | ¬p:?x∈R,log2(3x+1)>0 | B. | ¬p:?x∈R,log2(3x+1)>0 | ||
| C. | ¬p:?x∈R,log2(3x+1)≤0 | D. | ¬p:?x∈R,log2(3x+1)≤0 |
6.从一批苹果中随机抽取100个作为样本,其重量(单位:克)的频数分布表如下:
(1)在频率分布直方图中,求分组重量在[85,95)对应小矩形的高;
(2)利用频率估计这批苹果重量的平均数.
(3)用分层抽样的方法从重量在[85,95)和[105,115)的苹果中抽取5个,从这5个苹果任取2个,求重量在这两个组中各有1个的概率.
| 分组(重量) | [75,85) | [85,95) | [95,105) | [105,115) |
| 频数(个) | 15 | 30 | 35 | 20 |
(2)利用频率估计这批苹果重量的平均数.
(3)用分层抽样的方法从重量在[85,95)和[105,115)的苹果中抽取5个,从这5个苹果任取2个,求重量在这两个组中各有1个的概率.
20.已知三棱锥P-ABC的三条侧棱两两互相垂直,且AB=$\sqrt{5}$,BC=$\sqrt{7}$,AC=2,则此三棱锥的外接球的体积为( )
| A. | $\frac{8}{3}$π | B. | $\frac{8\sqrt{2}}{3}$π | C. | $\frac{16}{3}$π | D. | $\frac{32}{3}$π |
3.函数f(x)=x3+x-2有 ( )个零点.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
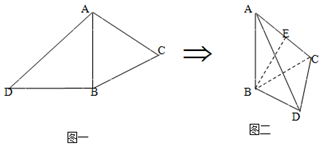 如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿AB折起,使得面ABD⊥面ABC,如图二,E为AC的中点
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿AB折起,使得面ABD⊥面ABC,如图二,E为AC的中点