题目内容
16.已知函数f(x)=(x-2)ex(I)求f(x)的单调区间;
(II)函数g(x)=ax2-2ax,若对一切x∈(2,+∞)有f(x)≥g(x)恒成立,求a的取值范围.
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)问题转化为a≤$\frac{{e}^{x}}{x}$在x∈(2,+∞)恒成立,令h(x)=$\frac{{e}^{x}}{x}$,根据函数的单调性求出a的范围即可.
解答 解:( I)f′(x)=(x-1)ex,
令f′(x)>0,解得:x>1,
令f′(x)<0,解得:x<1,
函数在(-∞,1)上单减,在(1,+∞)上单增;
( II)若对一切x∈(2,+∞)有f(x)≥g(x)恒成立,
则(x-2)ex≥ax(x-2),在(2,+∞)恒成立,
即a≤$\frac{{e}^{x}}{x}$在x∈(2,+∞)恒成立,
令h(x)=$\frac{{e}^{x}}{x}$,则h′(x)=$\frac{{e}^{x}(x-1)}{{x}^{2}}$>0,x∈(2,+∞),
故h(x)>h(2)=$\frac{{e}^{2}}{2}$,
则a≤h(2)=$\frac{{e}^{2}}{2}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
4.三棱锥S-ABC中,底面ABC为等腰直角三角形,BA=BC=2,侧棱SA=SC=2$\sqrt{3}$,二面角S-AC-B的余弦值为$\frac{\sqrt{5}}{5}$,则此三棱锥外接球的表面积为( )
| A. | 16π | B. | 12π | C. | 8π | D. | 4π |
11.已知“x>k”是“$\frac{3}{|x|}$<1”的充分不必要条件,则k的取值范围是( )
| A. | [3,+∞) | B. | [2,+∞) | C. | (3,+∞) | D. | (一∞,-3] |
5.若集合A={-1,0,1},B={y|y=x2,x∈A},则A∩B=( )
| A. | {0} | B. | {1} | C. | {0,1} | D. | {0,-1} |




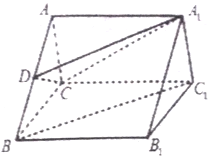 如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,过A1C作平面A1CD平行于BC1,交AB于D点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,过A1C作平面A1CD平行于BC1,交AB于D点.