题目内容

3．函数f（x）=x3+x-2有 （　　）个零点．
A．0B．1C．2D．3

分析 求出函数的极值，利用函数的性质，判断零点个数即可．

解答 解：函数f（x）=x3+x-2，可得f′（x）=3x2+1＞0，函数是单调增函数，所以函数的零点有1个．
故选：B．

点评 本题考查函数的零点的个数的判断，函数的单调性的应用，考查计算能力．

练习册系列答案
相关题目
11．已知“x＞k”是“$\frac{3}{|x|}$＜1”的充分不必要条件，则k的取值范围是（　　）
A．[3，+∞）B．[2，+∞）C．（3，+∞）D．（一∞，-3]
12．设a＞0，若函数y=$\frac{8}{x}$，当x∈[a，2a]时，y的范围为[$\frac{a}{4}$，2]，则a的值为（　　）
A．2B．4C．6D．8
9．执行如图所示的程序框图，则输出的S的值为（　　）
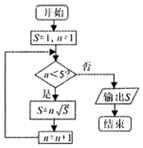
A．$4\sqrt{3\sqrt{2}}$B．$5\sqrt{4\sqrt{3\sqrt{2}}}$C．$5\sqrt{4}$D．$4\sqrt{3}$
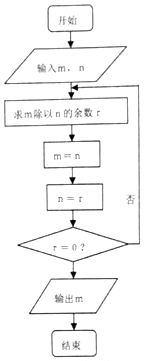16．如图程序框图的算法思路源于欧几里得名著《几何原本》中的“辗转相除法”，执行该程序框图，若输入m，n分别为225、135，则输出的m=（　　）
A．5B．9C．45D．90
8．已知函数f（x）=2f′（1）lnx-x，则f′（1）的值为1．
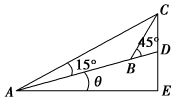15．如图所示，在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°，向山顶前进100m到达B处，又测得C对于山坡的斜度为45°，若CD=50m，山坡对于地平面的坡度为θ，则cosθ=$\sqrt{3}$-1．
12．在等比数列{an}中，a2=2，a5=16，记{an}的前n项和为Sn，则S10=（　　）
A．1024B．1023C．2048D．2046
13．已知函数f（x）是定义在R上的奇函数，当x＜0时，$f（x）={2^x}-{x^{\frac{1}{3}}}$，求当x＞0时f（x）的解析式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网