题目内容
如图，在长方体ABCD-A1B1C1D1中，若棱BB1=BC=1，AB=| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
考点：异面直线及其所成的角
专题：计算题,空间角
分析：用向量BA，BC，BB1分别表示向量BD1，AC，运用向量的数量积定义和模的性质，即可求出异面直线D1B和AC所成角的余弦值．
解答：
解：∵
=
+
+
，
=
-
，
∴|
|=
=
，
|
|=
=2
∴
•
=
•
-
2+
2-
•
+
•
-
•
=-3+1=-2，
∴异面直线D1B和AC所成角的余弦值，cosθ=|
|=
，
故选D．
| BD1 |
| BA |
| BC |
| BB1 |
| AC |
| BC |
| BA |
∴|
| BD1 |
| 3+1+1 |
| 5 |
|
| AC |
| 1+3 |
∴
| BD1 |
| AC |
| BA |
| BC |
| BA |
| BC |
| BC |
| BA |
| BB1 |
| BC |
| BB1 |
| BA |
∴异面直线D1B和AC所成角的余弦值，cosθ=|
| ||||
|
|
| ||
| 5 |
故选D．
点评：本题主要考察异面直线及其所成的角，运用空间向量的数量积求解，考查学生的运算求解能力．
练习册系列答案
相关题目
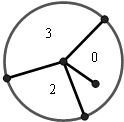如图所示，旋转一次的圆盘，指针落在圆盘中3分处的概率为a，落在圆盘中2分处的概率为b，落在圆盘中0分处的概率为c，（a，b，c∈（0，1）），已知旋转一次圆盘得分的数学期望为1分，则| 2 |
| a |
| 1 |
| 3b |
A、
| ||
B、
| ||
C、
| ||
D、
|
将正方形ABCD沿对角线BD折成一个直二面角，点C到达点C1，则异面直线AB与C1D所成角是（ ）
| A、90° | B、60° |
| C、45° | D、30° |
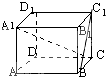如图，长方体ABCD-A1B1C1D1中，AB=AA1=2BC，则直线BC1与直线A1C所成角的余弦值为（ ）A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
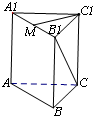如图，在直三棱柱ABC-A1B1C1的底面ABC中，CA=CB=1，∠BCA=90°，AA1=2，点M是A1B1的中点，则异面直线C1M与B1C所成角的余弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在矩形ABCD中，AB=2，BC=1，E为BC的中点，若F为该矩形内（含边界）任意一点，则
•
的最大值为（ ）
| AE |
| AF |
A、
| ||
| B、4 | ||
C、
| ||
| D、5 |
对于数25，规定第1次操作为23+53=133，第2次操作为13+33+33=55，如此反复操作，则第100次操作后得到的数是（ ）
| A、25 | B、250 |
| C、55 | D、133 |
正方体的八个顶点共可以连成28条直线，从这28条直线中任取2条直线，这2条直线恰好是一对异面直线．则这样不同的异面直线有多少对（ ）
| A、174 | B、87 |
| C、348 | D、84 |