题目内容
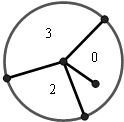 如图所示,旋转一次的圆盘,指针落在圆盘中3分处的概率为a,落在圆盘中2分处的概率为b,落在圆盘中0分处的概率为c,(a,b,c∈(0,1)),已知旋转一次圆盘得分的数学期望为1分,则
如图所示,旋转一次的圆盘,指针落在圆盘中3分处的概率为a,落在圆盘中2分处的概率为b,落在圆盘中0分处的概率为c,(a,b,c∈(0,1)),已知旋转一次圆盘得分的数学期望为1分,则| 2 |
| a |
| 1 |
| 3b |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:基本不等式
专题:不等式的解法及应用
分析:由数学期望可得3a+2b=1,可得
+
=(
+
)(3a+2b)=6+
+
+
,由基本不等式可得.
| 2 |
| a |
| 1 |
| 3b |
| 2 |
| a |
| 1 |
| 3b |
| 2 |
| 3 |
| 4b |
| a |
| a |
| b |
解答:
解:由题意可得数学期望为3a+2b+0×c=1,
∴
+
=(
+
)(3a+2b)
=6+
+
+
≥
+2
=
当且仅当
=
即a=
,b=
时取等号,
∴
+
的最小值为
故选:A.
∴
| 2 |
| a |
| 1 |
| 3b |
| 2 |
| a |
| 1 |
| 3b |
=6+
| 2 |
| 3 |
| 4b |
| a |
| a |
| b |
| 20 |
| 3 |
|
| 32 |
| 3 |
当且仅当
| 4b |
| a |
| a |
| b |
| 1 |
| 4 |
| 1 |
| 8 |
∴
| 2 |
| a |
| 1 |
| 3b |
| 32 |
| 3 |
故选:A.
点评:本题考查基本不等式,涉及数学期望的应用,属基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知向量
=(4,x),
=(2,4),若
=2
,则x=( )
| a |
| b |
| a |
| b |
| A、-2 | B、2 | C、-8 | D、8 |
在正方体ABCD-A1B1C1D1中,E是B1C1的中点,则异面直线DC1与BE所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
在△ABC中,A:B:C=4:1:1,则a:b:c=( )
A、
| ||
| B、2:1:1 | ||
C、
| ||
| D、3:1:1 |
 一个空间几何体的正视图,侧视图,俯视图都为全等的等腰直角三角形(如图所示),如果直角三角形的直角边长为1,那么这个几何体的外接球的体积为( )
一个空间几何体的正视图,侧视图,俯视图都为全等的等腰直角三角形(如图所示),如果直角三角形的直角边长为1,那么这个几何体的外接球的体积为( )| A、3π | ||||
B、
| ||||
| C、12π | ||||
D、
|
 如图,在长方体ABCD-A1B1C1D1中,若棱BB1=BC=1,AB=
如图,在长方体ABCD-A1B1C1D1中,若棱BB1=BC=1,AB=| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|