题目内容
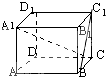 如图,长方体ABCD-A1B1C1D1中,AB=AA1=2BC,则直线BC1与直线A1C所成角的余弦值为( )
如图,长方体ABCD-A1B1C1D1中,AB=AA1=2BC,则直线BC1与直线A1C所成角的余弦值为( )A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出直线BC1与直线A1C所成角的余弦值.
解答:
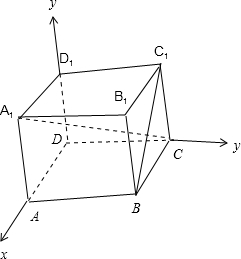 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,
建立空间直角坐标系,
∵AB=AA1=2BC,设BC=1,
∴B(1,2,0),C1(0,2,2),
A1(1,0,2),C(0,2,0),
∴
=(-1,0,2),
=(-1,2,-2),
设直线BC1与直线A1C所成角为θ,
则cosθ=|cos<
,
>|=|
|=
.
∴直线BC1与直线A1C所成角的余弦值为
.
故选:C.
 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
∵AB=AA1=2BC,设BC=1,
∴B(1,2,0),C1(0,2,2),
A1(1,0,2),C(0,2,0),
∴
| BC1 |
| A1C |
设直线BC1与直线A1C所成角为θ,
则cosθ=|cos<
| BC1 |
| A1C |
| 1+0-4 | ||||
|
| ||
| 5 |
∴直线BC1与直线A1C所成角的余弦值为
| ||
| 5 |
故选:C.
点评:本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 一个空间几何体的正视图,侧视图,俯视图都为全等的等腰直角三角形(如图所示),如果直角三角形的直角边长为1,那么这个几何体的外接球的体积为( )
一个空间几何体的正视图,侧视图,俯视图都为全等的等腰直角三角形(如图所示),如果直角三角形的直角边长为1,那么这个几何体的外接球的体积为( )| A、3π | ||||
B、
| ||||
| C、12π | ||||
D、
|
已知P是双曲线
-
=1(a>0,b>0)的右支上一点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,下列命题正确的是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、双曲线的焦点到渐近线的距离为a | ||
B、若|PF1|=e|PF2|,则e的最大值为
| ||
| C、△PF1F2的内切圆的圆心的横坐标为b | ||
D、若∠F1PF2的外角平分线交x轴与M,则
|
同时抛掷三枚均匀的硬币,一枚反面朝上,二枚正面朝上的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
甲、乙两人从4门课程中各选修1门,则甲、乙所选的课程不相同的选法共有( )
| A、6种 | B、12种 |
| C、30种 | D、36种 |
 如图,在长方体ABCD-A1B1C1D1中,若棱BB1=BC=1,AB=
如图,在长方体ABCD-A1B1C1D1中,若棱BB1=BC=1,AB=| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
“x=4”是“x2-4x=0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
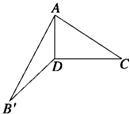 如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二面角大小是( )
如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二面角大小是( )| A、30° | B、60° |
| C、90° | D、120° |