题目内容
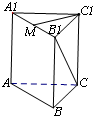 如图,在直三棱柱ABC-A1B1C1的底面ABC中,CA=CB=1,∠BCA=90°,AA1=2,点M是A1B1的中点,则异面直线C1M与B1C所成角的余弦值为( )
如图,在直三棱柱ABC-A1B1C1的底面ABC中,CA=CB=1,∠BCA=90°,AA1=2,点M是A1B1的中点,则异面直线C1M与B1C所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:以点C为坐标原点,以CA,CB,CC1所在直线分别作为x,y,z轴,建空间直角坐标系,利用向量法能求出异面直线C1M与B1C所成角的余弦值.
解答:
解:以点C为坐标原点,以CA,CB,CC1所在直线分别作为x,y,z轴,
建空间直角坐标系,
则由题意知B1(0,1,2),C1(0,0,2),M(
,
,2),
∴
=(0,1,2),
=(
,
,0),
设所求角为θ,
则cosθ=
=
.
∴异面直线C1M与B1C所成角的余弦值为
.
故选:D.
建空间直角坐标系,

则由题意知B1(0,1,2),C1(0,0,2),M(
| 1 |
| 2 |
| 1 |
| 2 |
∴
| CB1 |
| C1M |
| 1 |
| 2 |
| 1 |
| 2 |
设所求角为θ,
则cosθ=
| ||||
|
|
| ||
| 10 |
∴异面直线C1M与B1C所成角的余弦值为
| ||
| 10 |
故选:D.
点评:本题考查异面直线所成角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
已知向量
=(4,x),
=(2,4),若
=2
,则x=( )
| a |
| b |
| a |
| b |
| A、-2 | B、2 | C、-8 | D、8 |
已知a、b、c为正实数,且2a+b=1,则s=2
-5a2-b2-c2+2ac的最大值为( )
| ab |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
同时抛掷三枚均匀的硬币,一枚反面朝上,二枚正面朝上的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
给出下列三个等式:f(x+y)=f(x)+f(y),f(xy)=f(x)+f(y),f(x+y)=f(x)f(y),下列函数中不满足其中任何一个等式的是( )
| A、f(x)=x |
| B、f(x)=log2x |
| C、f(x)=3x |
| D、f(x)=sinx |
 如图,在长方体ABCD-A1B1C1D1中,若棱BB1=BC=1,AB=
如图,在长方体ABCD-A1B1C1D1中,若棱BB1=BC=1,AB=| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
设集合A=B={1,2,3,4,5,6},分别从集合A和B中随机各取一个数x,y,确定平面上的一个点P(x,y),记“点P(x,y)满足条件x2+y2≤16”为事件C,则C的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=xa的图象过点(4,2),令an=
,n∈N*.记数列{an}的前n项和为Sn,则S2013=( )
| 1 |
| f(n+1)+f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
若cosα=
(
<α<2π),则cos(α+
)=( )
| ||
| 3 |
| 3π |
| 2 |
| 5π |
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|