题目内容
已知函数f(x)=
x3-x+
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)已知g(x)=-
x2+(a+1)x(a>0),若F(x)=f(x)+g(x)在[0,2]上有最大值1,试求实数a的取值范围.
| 1 |
| 3 |
| 1 |
| 3 |
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)已知g(x)=-
| a+1 |
| 2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)求函数f(x)的导数,利用函数的单调性和导数之间的关系即可求出函数的单调区间;
(Ⅱ)求函数F(x)的导数,根据函数的最值和导数之间的关系,即可得到结论.
(Ⅱ)求函数F(x)的导数,根据函数的最值和导数之间的关系,即可得到结论.
解答:
解:(Ⅰ)∵f(x)=
x3-x+
,
∴f′(x)=x2-1,
由f′(x)=x2-1>0,解得x>1或x<-1,
由f′(x)=x2-1<0,解得-1<x<1,
即函数f(x)的单调增区间为(1,+∞),(-∞,-1),单调递减区间为(-1,1);
(Ⅱ)∵g(x)=-
x2+(a+1)x(a>0),
∴F(x)=f(x)+g(x)=
x3-x+
-
x2+(a+1)x=
x3-
•x2+ax+
,
则F′(x)=x2-1-(a+1)x+a+1=x2-(a+1)x+a=(x-1)(x-a),
若0<a<1,
由F′(x)>0,解得x>1或x<a,此时函数单调递增,
由F′(x)<0,解得a<x<1,此时函数单调递减,
∵F(x)在[0,2]上有最大值 1,F(2)=1,
∴F(a)≤1,即a3-3a2+4≥0,
令g(a)=a3-3a2+4,则g′(a)=3a2-6a=3a(a-2),
∴g′(a)<0,
∴g(a)>g(1)=0,即0<a<1;
当a=1时,F′(x)=x2-2x+1=(x-1)2≥0,F(x)≤F(2)=1成立;
当1<a<2时,令F′(x)>0得0<x<1或a<x<2,
令F′(x)<0得1<x<a,F(2)=1,
∵F(x)在[0,2]上有最大值 1,∴F(1)≤1,即
-
+a+
≤1,解得a≤
,
∴1<a≤
,
当a≥2时,由F(x)的单调性知F(x)max=F(1)>F(2),故不成立;
综上,实数a的范围是0<a≤
.
| 1 |
| 3 |
| 1 |
| 3 |
∴f′(x)=x2-1,
由f′(x)=x2-1>0,解得x>1或x<-1,
由f′(x)=x2-1<0,解得-1<x<1,
即函数f(x)的单调增区间为(1,+∞),(-∞,-1),单调递减区间为(-1,1);
(Ⅱ)∵g(x)=-
| a+1 |
| 2 |
∴F(x)=f(x)+g(x)=
| 1 |
| 3 |
| 1 |
| 3 |
| a+1 |
| 2 |
| 1 |
| 3 |
| a+1 |
| 2 |
| 1 |
| 3 |
则F′(x)=x2-1-(a+1)x+a+1=x2-(a+1)x+a=(x-1)(x-a),
若0<a<1,
由F′(x)>0,解得x>1或x<a,此时函数单调递增,
由F′(x)<0,解得a<x<1,此时函数单调递减,
∵F(x)在[0,2]上有最大值 1,F(2)=1,
∴F(a)≤1,即a3-3a2+4≥0,
令g(a)=a3-3a2+4,则g′(a)=3a2-6a=3a(a-2),
∴g′(a)<0,
∴g(a)>g(1)=0,即0<a<1;
当a=1时,F′(x)=x2-2x+1=(x-1)2≥0,F(x)≤F(2)=1成立;
当1<a<2时,令F′(x)>0得0<x<1或a<x<2,
令F′(x)<0得1<x<a,F(2)=1,
∵F(x)在[0,2]上有最大值 1,∴F(1)≤1,即
| 1 |
| 3 |
| a+1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 3 |
∴1<a≤
| 5 |
| 3 |
当a≥2时,由F(x)的单调性知F(x)max=F(1)>F(2),故不成立;
综上,实数a的范围是0<a≤
| 5 |
| 3 |
点评:本题主要考查函数的单调性,最值和导数之间的关系,考查学生的运算能力,综合性较强运算量较大.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 如图,在长方体ABCD-A1B1C1D1中,若棱BB1=BC=1,AB=
如图,在长方体ABCD-A1B1C1D1中,若棱BB1=BC=1,AB=| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
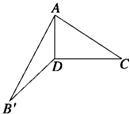 如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二面角大小是( )
如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二面角大小是( )| A、30° | B、60° |
| C、90° | D、120° |
若cosα=
(
<α<2π),则cos(α+
)=( )
| ||
| 3 |
| 3π |
| 2 |
| 5π |
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|