题目内容
正方体的八个顶点共可以连成28条直线，从这28条直线中任取2条直线，这2条直线恰好是一对异面直线．则这样不同的异面直线有多少对（ ）
| A、174 | B、87 |
| C、348 | D、84 |
考点：排列、组合及简单计数问题
专题：应用题,排列组合
分析：分类讨论其中直线异面的情况，可得异面直线的组数．
解答：
解：分类讨论：
①、棱与棱异面：每条棱有4条棱与其异面，共有情况
×12×4=24组，
②、棱与面对角线异面：每条棱有6条面对角线与其异面，共有情况12×6=72组，
③、棱与体对角线异面：每条棱有2条面对角线与其异面，共有情况12×2=24组，
④、面对角线与面对角线异面：每条面对角线与5条面对角线异面，共有情况
×12×5=30组，
⑤、面对角线与体对角线异面：每条面对角线与2条面对角线异面，共有情况12×2=24组，
则异面直线的组数为24+72+24+30+24=174组，
故选：A．
①、棱与棱异面：每条棱有4条棱与其异面，共有情况
| 1 |
| 2 |
②、棱与面对角线异面：每条棱有6条面对角线与其异面，共有情况12×6=72组，
③、棱与体对角线异面：每条棱有2条面对角线与其异面，共有情况12×2=24组，
④、面对角线与面对角线异面：每条面对角线与5条面对角线异面，共有情况
| 1 |
| 2 |
⑤、面对角线与体对角线异面：每条面对角线与2条面对角线异面，共有情况12×2=24组，
则异面直线的组数为24+72+24+30+24=174组，
故选：A．
点评：本题考查正方体的结构特征，涉及异面直线的判断方法，难点是正确分类讨论．
练习册系列答案
相关题目
一个空间几何体的正视图，侧视图，俯视图都为全等的等腰直角三角形（如图所示），如果直角三角形的直角边长为1，那么这个几何体的外接球的体积为（ ）| A、3π | ||||
B、
| ||||
| C、12π | ||||
D、
|
如图，在长方体ABCD-A1B1C1D1中，若棱BB1=BC=1，AB=| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
“x=4”是“x2-4x=0”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知函数f（x）=xa的图象过点（4，2），令an=
，n∈N*．记数列{an}的前n项和为Sn，则S2013=（ ）
| 1 |
| f(n+1)+f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知四棱锥P-ABCD中，底面ABCD是正方形，PA=AD=2，PA⊥平面ABCD，E，F分别是线段AB，BC的中点，则PE与FD所成角的余弦值为（ ）
A、-
| ||
B、-
| ||
C、
| ||
D、
|
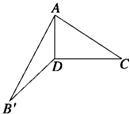如图所示，将等腰直角△ABC沿斜边BC上的高AD折成一个二面角，使得∠B′AC=60°．那么这个二面角大小是（ ）| A、30° | B、60° |
| C、90° | D、120° |