题目内容
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,-
<φ<
),其部分图象如图所示,将f(x)的图象纵坐标不变,横坐标变成原来的2倍,再向右平移1个单位得到g(x)的图象,则函数g(x)的解析式为( )

| π |
| 2 |
| π |
| 2 |

A、g(x)=sin
| ||
B、g(x)=sin
| ||
C、g(x)=sin(
| ||
D、g(x)=sin(
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式,再根据函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答:
解:由函数的图象可得A=1,
T=
•
=1-(-1)=2,∴ω=
.
再由五点法作图可得,
(-1)+φ=0,∴φ=
,函数f(x)=sin(
x+
).
将f(x)的图象纵坐标不变,横坐标变成原来的2倍,可得函数y=sin(
x+
)的图象;
再向右平移1个单位得到g(x)=sin[
(x-1)+
]=sin(
x+
)的图象,
故 函数g(x)的解析式为 g(x)=sin
(x+1),
故选:C.
| 1 |
| 4 |
| 1 |
| 4 |
| 2π |
| ω |
| π |
| 4 |
再由五点法作图可得,
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
将f(x)的图象纵坐标不变,横坐标变成原来的2倍,可得函数y=sin(
| π |
| 8 |
| π |
| 4 |
再向右平移1个单位得到g(x)=sin[
| π |
| 8 |
| π |
| 4 |
| π |
| 8 |
| π |
| 8 |
故 函数g(x)的解析式为 g(x)=sin
| π |
| 8 |
故选:C.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
已知cos(α-
)=
,则sin2α的值为( )
| π |
| 4 |
| 1 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
关于以下四个命题,不正确的是( )
①若函数y=2x的定义域是{x|x≤0},则它的值域为{y|y≤1}
②若函数y=
的定义域是{x|x>2},则它的值域为{y|y<
}
③若函数y=x2的值域是{y|0≤y≤4},则它的定义域一定是{x|-2≤x≤2}
④若函数y=log2x的值域是{y|y≤3},则它的定义域是{x|0<x≤8}.
①若函数y=2x的定义域是{x|x≤0},则它的值域为{y|y≤1}
②若函数y=
| 1 |
| x |
| 1 |
| 2 |
③若函数y=x2的值域是{y|0≤y≤4},则它的定义域一定是{x|-2≤x≤2}
④若函数y=log2x的值域是{y|y≤3},则它的定义域是{x|0<x≤8}.
| A、①②③ | B、②③④ |
| C、①③④ | D、①②④ |
函数y=|2x-1|的大致图象是( )
A、 |
B、 |
C、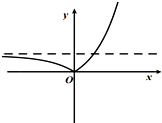 |
D、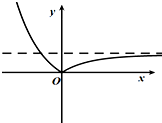 |
《张丘建算经》卷上第22题为:今有女善织,日益功疾,且从第2天起,每天比前一天多织相同量的布,若第1天织5尺布,现在一月(按30天计)共织390尺布,则每天比前一天多织( )尺布.(不作近似计算)
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a2+c2-b2=
ac,则∠B=( )
| 3 |
| A、60° | B、45° |
| C、120° | D、30° |
在下列命题中,正确的是( )
A、若|
| ||||||||
B、若|
| ||||||||
C、若
| ||||||||
D、若
|
三个实数a,b,c依次成公差不为零的等差数列,且a,c,b成等比数列,则
的值是( )
| a |
| b |
| A、-2 | B、2 | C、4 | D、-4 |